高考物理十大習題定理
1. 勻變速直線運動的4個重要推論

2. 初速度為零的勻變速直線運動的6個推論

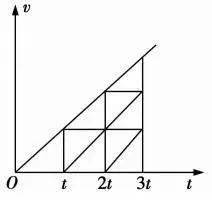
3. 物體處于平衡狀態的幾個推論

4. 物體在水平面和斜面上運動時的7個推論
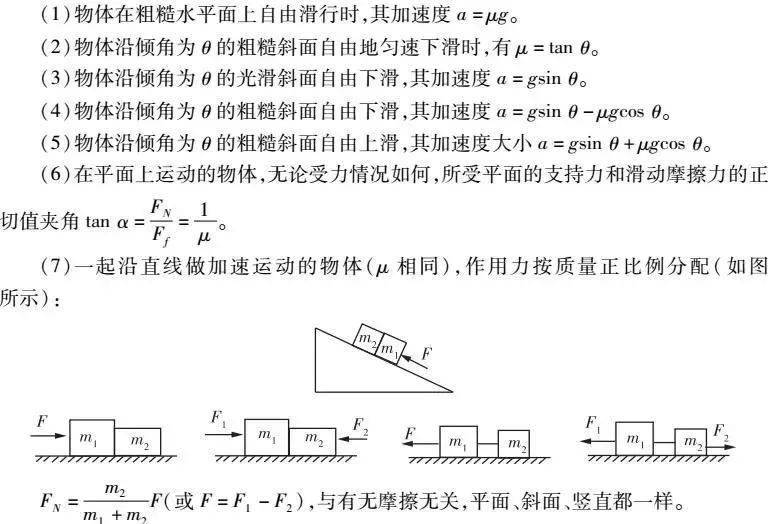
5. 平拋運動的4個重要推論

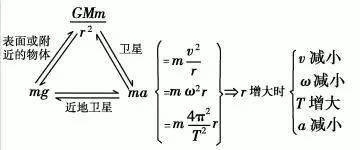
6. 天體運動中的三角等式關系
7. 彈性碰撞中的幾個重要結論

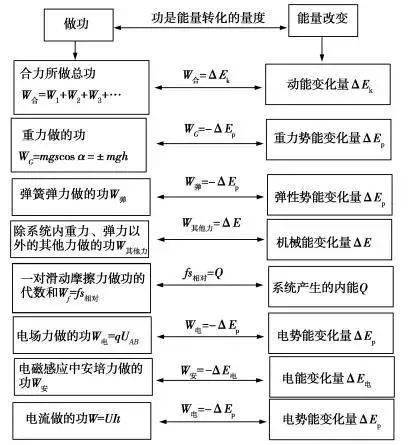
8. 八大功能關系
9. 電場力與能的性質
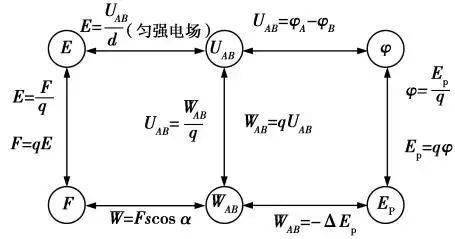

10. 電磁感應中的4個重要推論
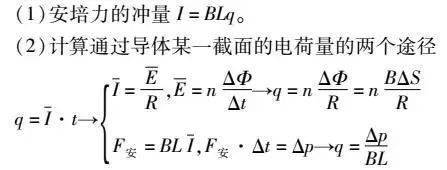
各種題型的關鍵突破口
“圓周運動”突破口關鍵是“找到向心力的來源”。
“做平拋運動,其突破口的關鍵之處在于這兩個矢量三角形,也就是位移三角形與速度三角形”。
“類平拋運動”突破口合力與速度方向垂直,并且合力是恒力!
突破“繩拉物問題”的關鍵在于速度的分解,那么該分解哪一個速度呢。所謂“實際速度”其實就是“合速度”,而合速度應當處于平行四邊形的對角線上,也就是說要分解合速度。
關于“萬有引力定律”的突破口,其關鍵之處在于“兩大思路” 。其一,F萬=mg這種情況適用于任何狀況,需要留意當涉及“衛星”或者“類衛星”的物體時,其中的g應當是該衛星所在位置處的g 。其二,F萬=Fn僅僅適用于“衛星”或者“類衛星” 。
理解萬有引力定律變軌問題的突破口,是借助離心以及向心來達成!(其中關鍵的字眼有:加速,減速,噴火)。
求各類星體的“第一宇宙速度”,其突破口的關鍵之處在于,軌道半徑乃是星球半徑 !
在受力分析時,其突破口在于“防止漏力”,也就是要去尋找施力物體,要是找不到施力物體,那么此力就不存在。還有“防止多力”,這需要按順序進行受力分析。(要分清“內力”與“外力”,其中內力不會改變物體的運動狀態,而只有外力才會改變物體的運動狀態。)。
三個共點力平衡問題的動態分析突破口矢量三角形法
從“加速度”這個角度,以及“受力”這個方面,來對“單個物體”超失重的突破口予以理解 。
“系統”里,只要有一個物體出現超、失重情況,那么整個系統就會被認為處于超、失重狀態,這個突破口系統就是這樣的標點符號。
機械波向前傳播的進程,就是波向前平移的進程,“質點振動方向”跟“波的傳播方向”的關系是“上山抬頭,下山低頭”,波源之后的質點進行的都是受迫振動,“受的是波源的迫”,所有質點起振方向都相同,波速僅僅取決于介質,頻率僅僅取決于波源。
關于“動力學”方面的問題,其突破口在于,當看到時要進行“受力”分析從而明確“運動情況”,而當看到“運動”的時候高中物理推論,則要想到與之相關的“受力情況”。

判斷正負功的突破口之一,要看F與S兩者之間的夾角情況,要是夾角是銳角,那么就做正功,要是夾角是鈍角,那就做負功,要是夾角為直角,便不做功 。判斷正負功的突破口之二,要看F與V兩者之間的夾角狀況,要是夾角是銳角,那么就做正功,若是夾角是鈍角,那就做負功物業經理人,要是夾角為直角,便不做功 。判斷正負功的突破口之三,要看是“動力”還是“阻力”,要是是動力,那么就做正功,要是是阻力,那就做負功 。
首先要把握住“游標卡尺”以及“千分尺(螺旋測微器)”讀數的突破口,也就是要明晰這兩種尺子的意義,其意義在于“可動刻度中的10分度、20分度、50分度,所表達的是將主尺上的最小刻度進行10等份、20等份、50等份”,之后先憑借主尺讀出整數部分,接著再依據可動刻度讀出小數部分,要格外留意單位。
解答物理圖像問題的突破口,有方法一,即定性法,首先要看清楚縱、橫坐標,以及它們各自的單位,接著分析縱坐標是怎樣隨著橫坐標進行變化的,隨后查看特殊的點、斜率。(倘若這種方法能夠解決問題,那它就是速度最快的解決辦法)還有方法二,也就是定量法高中物理推論,要羅列出數學函數表達式,依據數學知識,結合物理規律,直接給出解答。(這種方法是在定性法無法解決問題的時候,進行定量得出結果,最為精準)就像“U=-rI+E”與“y=kx+b”比對那樣。
關于理解重力勢能、電勢能、電勢、電勢差這些概念的突破口,在于將重力場與電場進行對比,也就是把高度與電勢相對比,把高度差與電勢差相對比。
對于含容電路能實現動態分析,其突破口要利用到公式,公式為C等于Q除以U,Q除以U又等于εs除以4πkd,εs除以4πkd中的E等于u除以d,u除以d還等于4πkQ除以εs 。
寫出閉合電路動態分析突破口的公式I=E/(R+r),之后從干路開始到支路,依據不變量去判斷變化量。
能夠作為楞次定律突破口的是,其中的“阻礙”以及“變化”,(就如同那句“相見時難別亦難”所表達的復雜情感一樣!)也就是新產生的磁場會對原磁場的變化起到阻礙作用。
將“環形電流”與“小磁針”的突破口進行互相等效處理,若把環形電流等效成小磁針,那么就能依據“同極相斥、異極相吸”去判斷環形電流的運動情形,要是把小磁針等效為環形電流,那么就能夠按照“同向電流相吸、異向電流相斥”來判斷小磁針的運動狀況。
“小磁針指向”判斷最佳突破口畫出小磁針所在處的磁感線!
在復合場里,物理存在“最高點”以及“最低點”,其突破口在于,與合力方向相重合的直徑的兩端點,就是物理的最高(低)點。
將洛倫茲力問題進行處理時,其突破口在于,確定圓心所在位置,找出半徑線段長度,描繪物體運動軌跡,構建直角三角形圖形,。
面對帶電粒子于磁場里做圓周運動的情況,其突破口其一乃是去繪制軌跡,這繪制軌跡的操作必須要嚴格依照規范來進行作圖,通過這樣精細的作圖,進而從中尋覓幾何關系。而這個問題解決辦法的另外一部分,才是去列出方程。
帶電粒子于復合場里運動問題的突破口在于,重力、勻強電場中的電場力皆是恒力,要是粒子的速度大小有變化,或者速度方向有變化,那么洛倫茲力就會產生變化,進而對粒子的運動以及受力情況造成影響!
電磁感應現象有兩個典型實際模型作為突破口 ,一個是“棒” ,其公式為E=BLv ,通過右手定則來判斷電流方向 ,其中“切割磁干線的那部分導體”相當于是“電源” ;另一個是“圈” ,公式是E=nΦ/t ,依據楞次定律判斷電流方向 ,“處在變化的磁場中的那部分導體”相當于“電源” 。
在“霍爾元件”里,判斷電勢高低的突破口在于,究竟是誰在運動,只要是誰運動,那么誰就會受到洛倫茲力!也就是說,運動著的電荷,不管其是正電荷還是負電荷,都會受到洛倫茲力。
當帶點離子,在重力不計的情況下,進入圓形磁場區域,在洛倫茲力的作用下,于磁場中運動,其軌跡半徑等于圓形磁場半徑時,離子出現的情況是,一次從某一點入射隨后平行引出,或者一次平行入射隨后從某一點引出 。
