說到橢圓,就必須說到天體的運動。 在高中物理中,涉及橢圓的開普勒三定律實際上非常困難。 這句話我好像在哪里說過過!
今天主要和朋友們分享一個利用橢圓的定義來解決物理問題的數學方法。
橢圓定義為平面上一點到兩個固定點的距離之和等于固定值的點的軌跡稱為橢圓。 兩個固定點是焦點高中物理天體,距離之和是長軸2a。
這是高中數學中橢圓的定義,也是橢圓的第一個定義。
開普勒第一定律是行星繞太陽運行的軌道是橢圓,太陽位于橢圓的焦點。 當然,它也適用于繞行星運行的衛星。 那么,我們來看一個問題。
示例:假設一枚導彈從地球赤道發射并擊中北極。 求導彈的最小發射速度。 已知萬有引力常數為G,地球半徑為R。不考慮地球自轉和空氣阻力。
解:先畫個圖高中物理天體,如下圖所示,軌跡是橢圓。
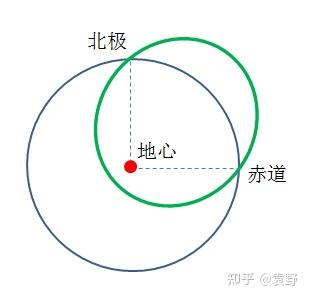
根據機械能守恒定律,導彈的機械能為:

E=-frac{GMm}{2a} ,
其中a是橢圓軌道的半長軸。
上述公式的推導有兩種方法:
1. 使用圓形軌道類比。
2.直接用橢圓軌道推導。 詳細內容參見《原野:橢圓軌道相關計算雜談》和《原野:用橢圓軌道證明開普勒第三定律》中的相關介紹。
因此,假設導彈的初速度為v_0,則:
由E=E_k+E_p可知,
-frac{GMm}{2a}=frac{1}{2}mv_0^2-frac{GMm}{R} ,
通過移動條款,我們得到,
frac{1}{2}mv_0^2=frac{GMm}{R}-frac{GMm}{2a} (1)
因此,最小化軌跡的半長軸a就足夠了。
如下圖所示,根據橢圓的定義,橢圓上一點到兩個焦點的距離之和就是長軸2a。 其中一個焦點是地球中心O。已知我們現在需要找到另一個焦點,使得“橢圓上的點到兩個焦點的距離之和最小”英語作文,顯然可以是由簡單的數學幾何關系可知,如下圖所示,垂直找到另一個焦點C。
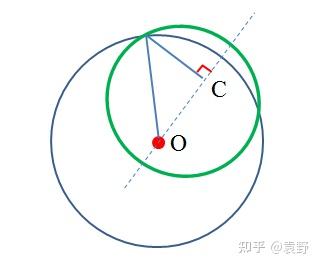
所以我們得到, 2a=R+frac{sqrt2}{2}R (2)
聯立式(1)和式(2)可得:
v_0=sqrt{frac{2GM}{R}(sqrt2-1)} 。
好吧,就是這樣!
哎呀,我最近好像有點不開心啊! 我怎樣才能讓自己快樂?
朋友們,我們下次再見!
