一、機械運動部分
(一)勻速直線運動的速度、路程、時間公式:
第一個,求取速度的公式是:v等于s除以t ;第二個,求取路程的公式是:s等于v乘以t ;第三個,求取時間的公式是:t等于s除以v 。
注意,v代表速度,其單位是米每秒或者千米每小時。s代表路程,單位是米或者千米。t代表時間,單位是秒或者小時 。
各量關系如下,當t處于一定狀態時,s和v呈現出成正比的關系;當s處于一定狀態后,t和v呈現出成反比的關系;當v處于一定狀態時,s和v呈現出成正比的關系。請注意,絕對不可以表述為v與s成正比或者與t成反比 。
(二)變速直線運動的平均速度:
你提供的內容似乎不太完整且有錯誤表述。請你檢查并補充完整準確的內容,以便我按照要求改寫 。
這似乎并不是一個完整的可改寫的句子內容呀,請你提供準確完整的句子以便我按照要求進行改寫 。
222(三)幾種特殊題型中的各量關系:
1、“回聲測距”問題:s=2.“火車過橋(洞)問題”:
(1)火車于通過橋之際,其所歷經的距離是:s等于s橋加上s車;(2)火車處于完全在橋上之時,其所經過的距離是要這樣計算:s等于s橋減去s車 。
3. 借助相對速度來求解的相關問題:【相對速度乃是——相對運動的兩個物體,以其中一個作為參照物時,另一物體相對于它而言的運動速度。當兩個物體處于同一條線或者相互平行的兩條線上進行運動的時候:】。
一種情況是,同向的時候,相對速度是,v同向等于v1加上v2 ;另一種情況是,異向的時候,相對速度是,v異向等于v大減去v小 。
追及問題方面,于研究追及問題這個情況時,為將問題予以簡化,常規是以被追及者當作參照物來看待的,追及所運用的時間指的是追及者憑“同向相對速度”來運動完他們之間“間距”所使用的時間。也就是:t追等于s間,s間 。
v同向時,取v大減去v小,s相對為s2。相向錯車時,s相對等于s1加s2 。
v異向=v1+v2 ,
t錯?相對
V同向V同向(2)相遇情況:朝著對方行進或者朝相反方向行進的物體,它們的相對速度是:V異向等于v1加上v2,相關的路程是s1加上s2 。
(3)錯車問題:1同向錯車:s相對=s1+s2 ,
v同向=v大-v小 ,
在研究水中物體運動的相遇以及追擊問題之時,一般會以水當作參照物,物體都會以相對于水的速度進行運動,如此能夠讓問題得到簡化,比如,在一條河水中存在漂浮著的一個百寶箱,在距離百寶箱處于等距離的上下游位置各有一艘小船,它們同時以相同的靜水速度朝著百寶箱行駛而去,那么哪一艘小船會先到達百寶箱所處位置呢 。
二、密度部分
(一)、物體的物重跟質量之間存在著這樣的關系:一是求重力,其公式為G等于mg ;二是求質量,質量等于G除以g。
注意,G代表重力,其單位是N,m代表質量,單位是kg,而g表示每kg(通常可取10N/kg),單位是N/kg 。
(二)、密度及其變形公式:
1、求取物質的密度情況是經由公式ρ等于m除以V來達成的。 2、求取物質的質量情況是通過公式m等于ρ乘以V得以實現的。 3、求取物質的體積情況是鑒于公式V等于m除以ρ來達成的。
注,m代表質量,其單位是kg也可是g,V代表體積,其單位是m或是cm,ρ代表密度,其單位是kg/m或者g/cm ,這里是3333 。
有這樣一些量的彼此之間的關系,當體積V保持固定不變的時候,質量m與密度ρ呈現出成正比的情況,當質量m保持恒定時,體積V和密度ρ呈現出成反比的狀況,當密度ρ為定值的時候,質量m與體積V呈現出成正比的態勢,要特別注意,絕對不能夠表述為密度ρ與質量m成正比或者與體積V成反比 。
(三)、存在這樣一個關于空心的疑難問題,有一個物體,它的體積設定稱作V物,其具備一定的質量,質量記為m物,而構成這個物體的物質有著特定的密度,密度被標記為ρ物質,需要據此來判定該物體是不是空心的 。
比較密度的做法為,計算物體的平均密度ρ物,其計算公式是ρ物=m物/V物,之后和組成該物體的物質密度ρ物質進行比較,若二者不相等那么該物體就是空心的,若二者相等那么該物體就是實心的。
首先,計算呢,對于擁有V物體積的該種物質,其質量m',計算方式為m'等于ρ物質乘以V物 ?接下來,把這個質量m',跟物體質量m物去做比較 。假如不相等,那就表明是空心的 ;要是相等,那就意味著是實心的 。并且呀,空心體積V空的計算方式是,用m'減去m物的差,再除以ρ物質 。
3、進行體積比較:算出質量是m物的該種物質所應具備的實心體積V實,這里V實等于m物除以ρ物質,之后將其與物體體積V物去做比較,若二者不相等那就表明是空心的,要是相等則意味著是實心的。并且空心體積V空乃是V物減去V實。【這是計算空心體積常用的方法】。
在混合密度問題當中,存在相關情況,即有兩種物質,這兩種物質各自密度分別是ρ1以及ρ2,之后它們進行混合操作,并且假設混合之后體積維持不變 。
則一定有:?混?m總m?m2
你提供的內容似乎并不是一個規范的可理解的句子,請你檢查或重新清晰準確地表述一下,以便我能按照要求進行改寫 。
?總?1?1?1V總V?V2V2
三、壓強浮力部分
壓強的定義式子是p=F/S ,它于固、液、氣體而言都是適用的,前提是只要清楚壓力F以及受力面積S。
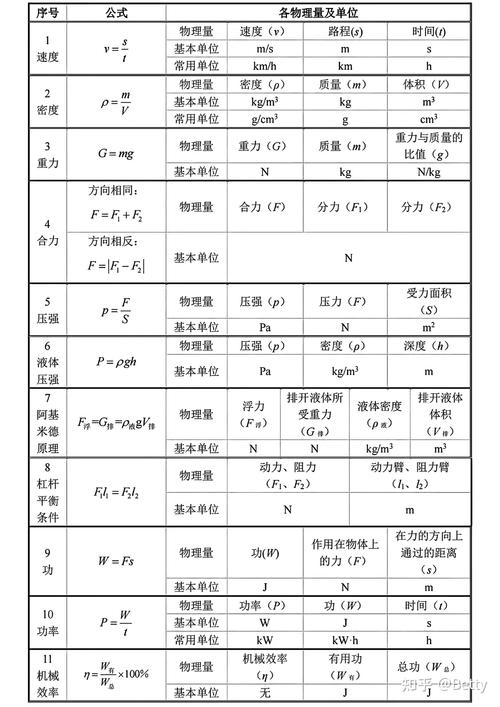
關系如下:當S保持恒定的時候,p跟F呈現為正比例關系;當F處于一定狀態時,p和S形成反比例關系;要是p固定不變,F和S呈現出正比例關系。
2、關于液體壓強,其公式為p=ρgh,在這里h指的是深度【存在這樣的變式: A、用于求密度時,公式為??pp ;B、用于求深度時,公式為h?】。
gh?g【各個量之間的關系是,當h保持一定的時候,p和ρ呈現出成正比的關系;在ρ處于一定狀態時,p和h呈現出成正比的關系;當p處于一定狀態時,h和ρ呈現出成反比的關系】。
3、求壓力:(1)F等于p乘以S,p又等于ρ乘以g乘以h,所以F等于ρghS(不管處于何種狀況,只要清楚壓強以及受力面積,這種情況下就都能夠運用此公式來計算壓力)。
存在這樣一個公式,即F等于G ,此公式僅僅適用于這樣的情況,那就是處于自由靜止狀態,可以是固體對水平臺面所產生的壓力,也可以是在水平臺面上的柱狀容器當中的液體,朝著容器底部所產生的壓力 。
4、求受力面積:S=F/p
23【說明:于以上公式里,各個量的單位,都必然得統一成為主單位,也就是:p對應Pa;F(G)對應N;ρ對應kg/m;S對應m;h對應m 】。
5、浮力的計算
(1)稱量法(示數差法):F浮=G-F
(2)公式法(原理法):F浮=G排=ρ排gV排
(3)平衡法,也就是浮體性質,其表述為:F浮等于G物 ,這里存在兩種情況,其一為漂浮,即V排小于V物,且ρ物小于ρ液 ;其二為懸浮物業經理人,即V排等于V物,且ρ物等于ρ液 。
(4)其他平衡:A、上拉平衡,由于G物等于F浮加上F拉,所以F浮等于G物減去F拉 。
B、往下拉(往下壓)達到平衡狀態時:物體所受的浮力等于物體自身的重力加上物體受到的向下的拉力或者壓力,其中G是物體的重力,F是物體受到的向下的拉力或壓力 。
C、沉底平衡:因為F浮+F支=G,所以F浮=G-F支
【幾個推論】
1、ρ物等于G除以G再乘以ρ液(理解為:處于浸沒狀態且在液體中下沉的物體,其所受到的重力是它所能受到的最大浮力的幾倍,那么物體密度乘以ρ等于液G減去F再除以F浮,其結果就是液體密度的幾倍) 。
當存在這樣一種情況,即物體為漂浮著的實心物體時,我們可以用到公式ρ物 = V浸×ρ液,這意味著浸入液體中的體積若是物體總體積的幾分之幾,相應地,該物體的密度便是液體密度的幾分之幾 。
置放V物3于其中,懸掛一下沉物,使其浸于液體里頭,容器對于桌面所增大的壓力ΔF等同于物體排開液體時所受到的重力,即是說ΔF等于G排,而G排又等于F浮 。
將特定的漂浮物放置于容器以內,把懸浮物置于容器之中時,容器針對桌面所增大給予壓力這一情況,它的數值ΔF等同于物體所遭受受到的重力,也就是ΔF等于G物,而G物又等于F浮,并且F浮還等于G排;。
把一個沉底物放置于容器之內,當物體沉至底部以后,容器針對桌面所增大的那個壓力ΔF等同于物體的重力,也就是說ΔF等于G物 。
四、功和機械能、簡單機械部分
1、功的公式
從定義式來講呀,是W等于Fs ,在已知了那個用來做功的力F ,以及這個力做功所產生的距離s的情況下 ,去求解功W的值 。
(2)變形式呢,A這種情況,存在公式F等于W除以s ,這里呢,是已知做功的量為W以及做功所經過的距離是s的前提下啦,去求解做這個功的力F哦。
B、s=W/F,【已知做功W及做功力F,求做功距離s】
注意,上述給定公式里,W代表功,其采用焦耳作為單位,也就是焦,記作J;F表示做功之時所用的力,該力采用牛頓作為單位,即牛,記作N;s指的是距離,這個距離是物體在做功力持續作用的情況下,沿著做功的力的方向所通過的距離,而且這個距離很可能小于物體實際移動的距離,它采用米作為單位,記作m 。
各量之間存在這樣的關系:當s保持一定的時候,W和F呈現出成正比的狀況,在F保持固定的時候,W又和s構成成正比的關系,而當W維持一定時,F則與s是成反比的狀態。
2、功率的公式
定義式為P等于W除以t ,【已知做功是W以及做功所花費的時間為t,求功的功率是P】 。
(2)存在變形式,其中一種是,A、W等于Pt,【給定了功率 P以及做功時間 t,要求出做功 W】 。
B、t=W/P,【已知做功W及功率P,求做功時間t】
在上述公式里,需留意,W代表功,其單位是焦耳,也就是焦,用J表示;P代表功率,單位是W,并且1W等于1J/s;t代表時間物理公式初中及單位,單位是s 。
63或者W——kWh(其中1kWh等于×10J);P——kW(這里1kW等同于10W);t——h(而1h等于3600s) 。
各量關系是,當t處于一定狀態時,W和P呈現出成正比的關系,當W處于一定狀態時,t和P呈現成反比的關系,當P處于一定狀態時,W和t呈現出成正比的關系。
它是這樣一種數量關系,即牽引力的功率,等于牽引力,與物體在牽引力方向上的速度,這二者的共同功效產生出的乘積 。
【變形式:A、F=P/v;B、v=P/F】
請留意,式子當中各個量的單位,必須統一為主要單位,也就是,F的單位是N,v的單位是m/s,P的單位是W 。
在各量關系當中,當F保持一定的情況下,P和v呈現出成正比的關系,當v處于一定狀態時,P與F是成正比的,而在P固定不變的時候,F跟v成反比。
3、杠桿平衡之條件:(1)乘積形式:F1L1等于F2L2 。于其中的具體意義為動力乘以動力臂等于阻力乘以阻力臂 。
(2)比例式:存在這樣一種關系,F1L2,它有著特定意義,即表示力與力臂成反比,或者說有著這樣的情況,動力臂是阻力臂的幾倍,那么動力就是阻力的幾分之一 。
F2邊的L1 ,【存在變形式:F1等于L2與L的乘積再除以F2 ;F2等于L1與F1乘積的倒數 ;L1等于L2的兩倍 ;L2等于L1的二分之一 】。
、機械效率:
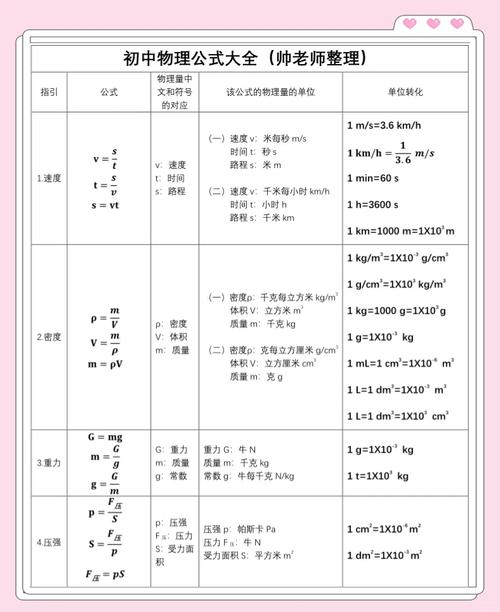
首先,有用功,就它呢,是那個目的功,然后呢,是在不借助機械的情境之下,直接針對物體去做的功,又或者呢,是做功機械針對物體所做的功 。
要是在空氣里頭提升物品不論采用何種辦法利用哪種機械那么會出現有用功等于物體重力乘以物體上升高度。
要是處于水中去提升物體的這種情況呢,則,有用功等于,物體重力減去浮力的差,再乘以物體被提升的高度 。
B、要是物體是水平移動的狀態(其目的在于應對物體因摩擦而產生的阻力來進行做功),那么:有用功W就等于摩擦力 f 與物體移動距離S物的乘積【即摩擦力 f 等于有用功W除以物體移動距離S物】 。
(2)額外功,那是指在使用機械之際,為了達成目的而沒辦法不額外去做的功 !
A、無論何種情況,一定有:W額=W總-W有用
B,針對斜面而言,有用功之外的額外功等于摩擦力與斜面長度的乘積【摩擦力等于額外功除以斜面長度;斜面長度等于額外功除以摩擦力】,。
C,當把輪和軸之間、輪和繩之間的摩擦以及繩的重量都不計算在內的時候,對于動滑輪、滑輪組提升物體來說,額外功等于動滑輪重力乘以物體被提升的高度,且可據此得出動滑輪重力等于額外功除以物體被提升的高度 。
(3)總功,也就是使用機械時整個過程所做的功,是人針對機械所實施的做功行為,是動力機械針對做功機械所開展的做功動作 。
A、人對機械所做的功等同于總功,W總之值等于F乘s,其中F是那個進行做功的力,s是該做做功力通過的距離 。
B、動力機械在做功這個行為發生的時候,存在這樣的關系:W總既等于此時的P總與t相乘 ,舉例來說:功率P總就是抽水機對外輸出的功率,抽水所經歷的時長是t 。
C、W總=W有用+W額
(4)機械效率
這部分內容似乎不太完整且表述混亂,不太明確要準確改寫的具體內容及要求,請提供更清晰準確的句子以便能更好地完成對其的改寫 。
W總?(5)機械效率的推導式:
效率等于有用功比上總功,有用功通過有用功率乘以時間得出,其變形式為功率等于效率乘以總功率,總功率等于有用功率除以效率。,,,,,,,,,,,。
W總,P總之中的tP總,?表示W有用,而W有用被定義為Gh,還有一種情況是W有用被定義為Fs阻物,(6)動力機械做功過程呈現為,η等于用舉高、提升物體時的W有用除以W總,或者η等于用平移物體時的W有用除以W總 。
W總PtW總P總t總(一)滑輪、滑輪組機械效率的運算
1、適用于動滑輪、滑輪組勻速豎直提升重物時則有:
有用功W有所對應的效率η等于,其變形式為有用功W有等于效率η乘以總功W總,總功W總等于有用功W有除以效率η,此為普遍適用情況, 。
W總?W有用 推導式η=推導過程:η====
有這樣一組變形式,其中一個是:F 等于 GG;還有一個是:n 等于;另外還有一個是G 等于?nF ,這里面的 G 表示的是物體重力,F 表示的是繩自由端的拉力,n 表示的是承擔阻力的繩子,n??F 。
股數,?表示機械效率】(普遍適用)
按這個推導式能夠看出,有關測量機械效率的實驗,只需測量出鉤碼那份重力G,以及繩子的拉力F,便能夠據此算出機械效率。
(1)如果不考慮摩擦和繩重:
當不考慮摩擦和繩重時適用,此時滑輪組動力和阻力的關系滿足 F 等于(物體重力與動滑輪重力之和除以物體重力),而機械效率 η 等于(物體重力除以物體重力與動滑輪重力之和)。
G物加上G動再除以n的推導過程是,效率等于有用功除以總功,有用功除以有用功與額外功之和,也等于有用功除以有用功加上額外功,即G物h除以G物h加上G動h,說明若不考慮摩擦和繩重,就只需克服動滑輪重做額外功,動滑輪和物體移動距離相同 。
2、利用滑輪組水平勻速移動物體時:
在任何情況都適用的是,有用功為W總時而效率等于W的那個值,或者當有用功是fs物(s物表示物體移動距離),總功是Fns物(這種情況時)效率等于f與f之比且等于f,變形式為,有F等于什么物理公式初中及單位,n等于什么,進而f等于效率與n和F的某種關系 。
nFn??Ffs物?f;【f表示物體受到的水平摩擦力】
;(此刻s物等于h),f加上G動,(2)水平移動物體之際同時將動滑輪提升起來了,而要是不把繩重以及繩輪、輪軸間的摩擦計算在內情況下:這里的機械效率等于W有用除以W總,W有用除以W有用加上W額,f乘以s物加上G動乘以h,(二)、斜面的機械效率:進行運算 。
1、?等于, 2、?等于W有用除以W總, W有用除以W總等于h乘以G除以G乘以h, 或者η等于乘以,具體是指h與l的比值, 【適用于任何情況】 。
(適合任何情況);有用Gh
??W有用?W額Gh?fL
當豎直提升重物且不計摩擦、繩重、動滑輪重時,繩端的拉力F等于物體重力G物與動滑輪重力G動之和除以承擔阻力的繩子段數n,即F等于(G物?G動)除以n ,當不計摩擦、繩重時,F等于物體重力G物除以承擔阻力的繩子段數n ,這里F是繩端的拉力,G物是物體重力,G動表示動滑輪重力,n是承擔阻力的繩子段數 。 , 。 。 。 。 ! ? 。
變為形式的情況是這樣的,G 物等于 nF,這里面是不算摩擦、繩重以及動滑輪重的;然后 G 物又等于 nF 減去 G 動;還有 G 動等于 nF 減去 G 物,這兩種情況都是不算摩擦和繩重的 。
B、在進行水平移動物體這個操作的時候:F等于11F阻,而F阻又等于f,這里的f指的是物體所受到的摩擦力,并且在這種情況下不考慮輪重、繩重以及其他的摩擦干擾;其變形式為:f等于nF,。
nn4、S繩=nS物
v繩=nv物(n是繩子股數)
