
機(jī)械效率是初八物理的最后一個(gè)難點(diǎn)。 主要難點(diǎn)在于簡(jiǎn)單機(jī)械的理解和機(jī)械效率的概念。 今天涼子老師就帶領(lǐng)大家學(xué)習(xí)另一種常見的簡(jiǎn)單機(jī)械——斜面。 機(jī)械效率,希望對(duì)您有所幫助。
您還可以觀看此視頻:
什么是斜角
斜面,即傾斜的平板,可以用相對(duì)較小的力將物體從較低的地方提升到較高的地方,但提升物體的路徑長(zhǎng)度也會(huì)增加。 斜面是古希臘人提出的六種簡(jiǎn)單機(jī)械之一。
在日常生活中斜面機(jī)械有哪些,我們經(jīng)常使用斜面。 行駛車輛的坡度是普通坡度。 卡車裝載大件貨物時(shí),常在卡車后部斜放置一塊木板,將貨物沿木板向上推。 坡度原理也被應(yīng)用。 日常生活中使用的螺釘也是斜角原理的一個(gè)很好的體現(xiàn)。 其他還有樓梯、登機(jī)橋、自動(dòng)扶梯、蜿蜒道路等。

下圖中的機(jī)器是利用斜面原理制造的阿基米德螺旋機(jī)器。 在我國(guó),古人發(fā)明的黃帝泵與此類似。

阿基米德螺旋機(jī)
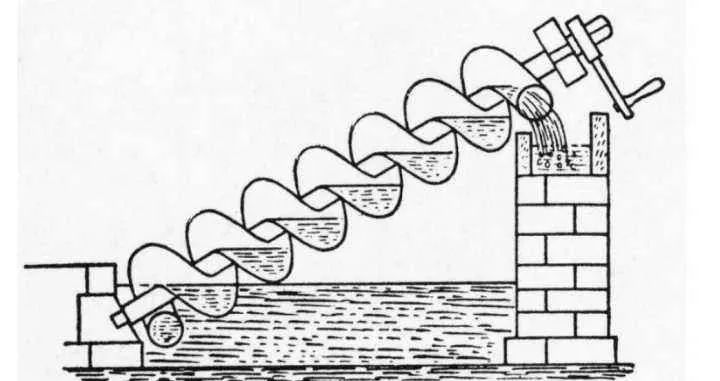
黃帝泵
如果斜面的斜率越小,即斜面與水平面的夾角越小,則需要對(duì)物體施加的力越小,但移動(dòng)的距離也會(huì)越長(zhǎng); 反之亦然。
請(qǐng)觀看動(dòng)畫:
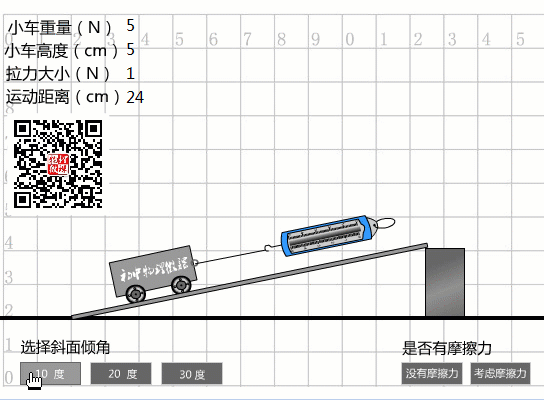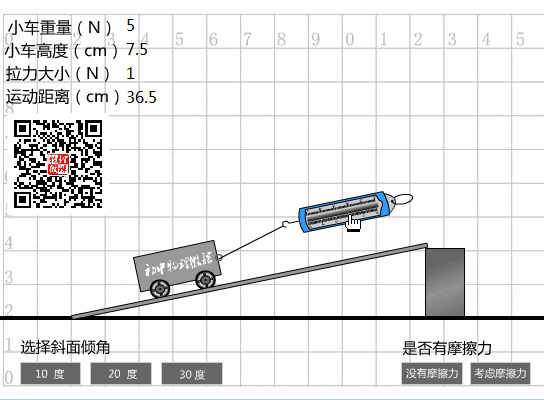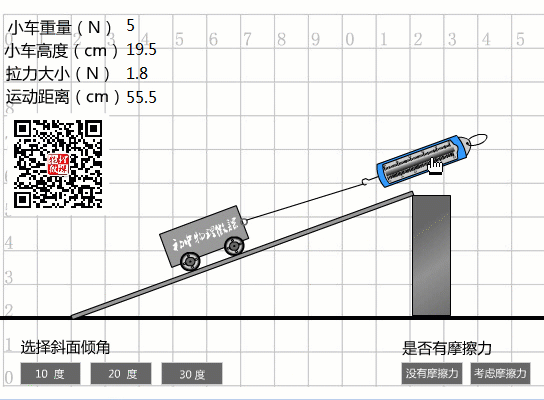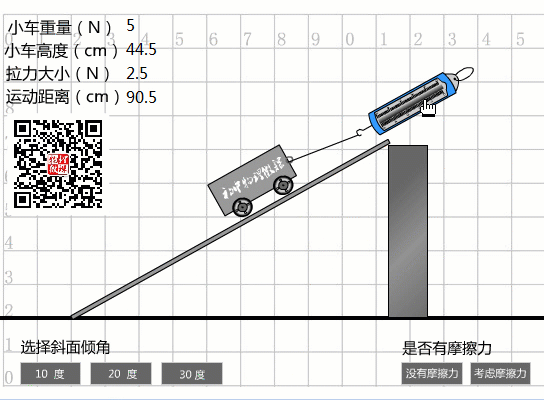
坡度越小,越容易省力。
在沒(méi)有摩擦的情況下,坡度為10度時(shí),拉力僅為1N,坡度為20度時(shí),拉力為1.8N,坡度為30度時(shí),拉力為2.5N。
坡口機(jī)械效率
斜面機(jī)也是一種常見的簡(jiǎn)單機(jī)械。 那么它的機(jī)械效率如何計(jì)算呢? 不同坡度的斜面有什么不同的特點(diǎn)?
如果不考慮任何摩擦阻力,斜面的機(jī)械效率為100%。 我們以30度斜面為例,將物體抬高20厘米。 從模擬動(dòng)畫可以看出:
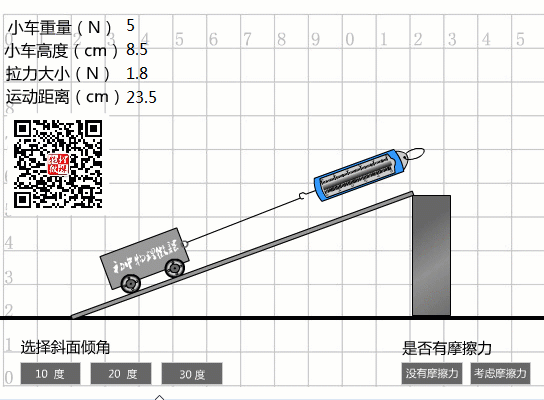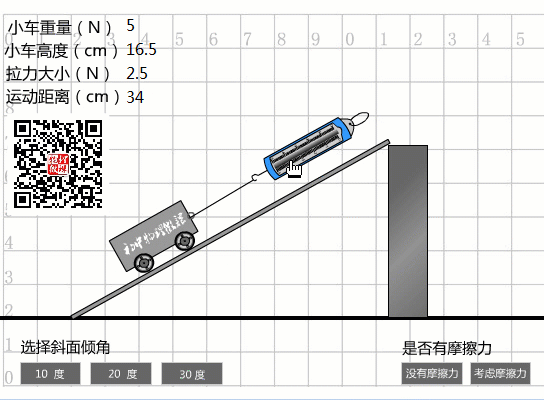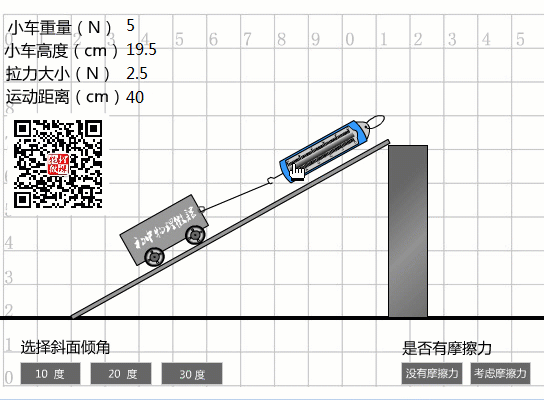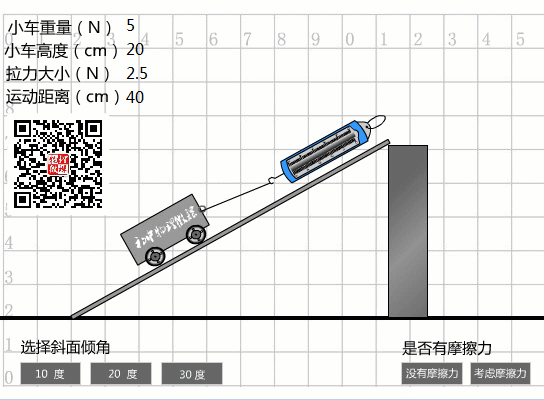
當(dāng)沒(méi)有摩擦?xí)r,斜面的機(jī)械效率等于100%
完成任務(wù)所需的功(即有用功):
W=Gh=5N×0.2m=1J
我們拉車時(shí)實(shí)際做的功(即總功):
W總計(jì)=Fs=2.5N×0.4m=1J。
因此其機(jī)械效率為:
η0=Whas/=1J/1J=100%。
然而,在現(xiàn)實(shí)生活中,使用真實(shí)的斜面時(shí)斜面機(jī)械有哪些,一些摩擦是不可避免的。 如果這個(gè)過(guò)程中為了克服摩擦而做功(即額外做功),那么斜面的機(jī)械效率必然小于100%。
斜面機(jī)械效率特點(diǎn)
現(xiàn)在,我們的問(wèn)題是:實(shí)際上,不同坡度的坡度之間的機(jī)械效率是否存在差異?
我們來(lái)做一個(gè)實(shí)驗(yàn):
我們這個(gè)實(shí)驗(yàn)的任務(wù)是將5N的小車?yán)?0cm的高度。 任務(wù)確定了,那么使用任意斜面時(shí),有用功仍等于1焦耳。 但在不同坡度的斜坡上完成這個(gè)任務(wù)時(shí),我們實(shí)際做的功(即總功)是一樣的嗎?
1、選擇10度坡度時(shí),從圖中數(shù)據(jù)可以看出:
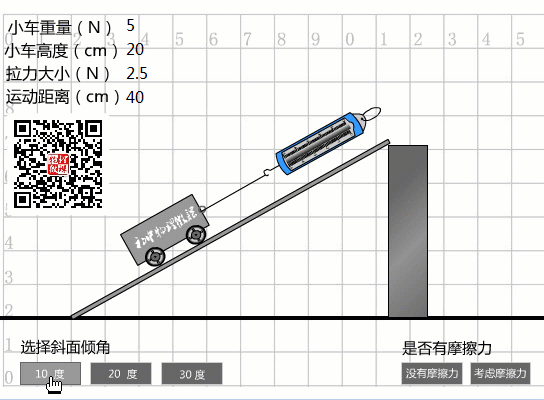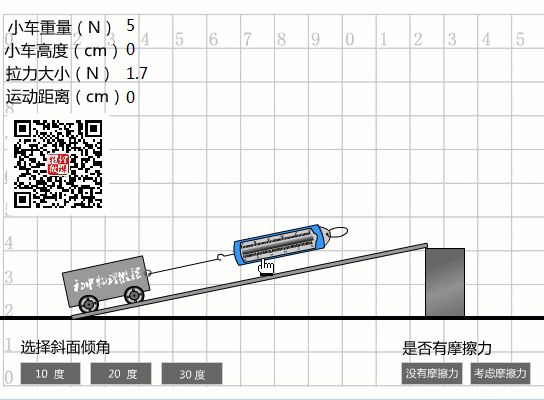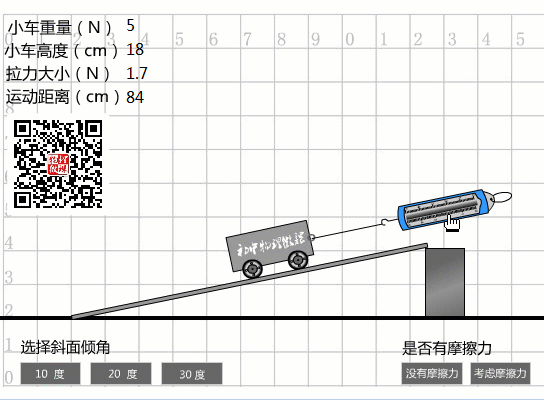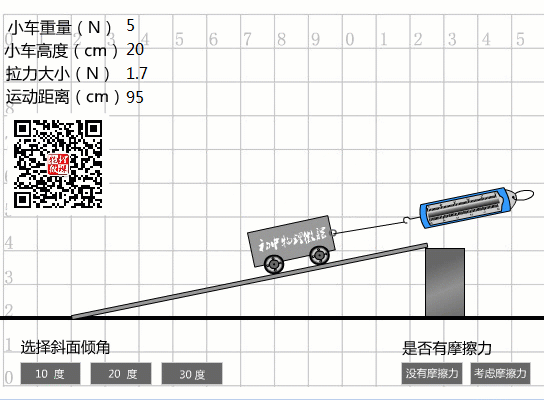
斜度為10度時(shí)的機(jī)械效率
我們拉車的實(shí)際工作是:
W總計(jì)=Fs=1.7N×0.95m=1.6J。
因此其機(jī)械效率為:
η1=Whas/=1J/1.6J=62.5%。
當(dāng)選擇20度坡度時(shí),從圖中數(shù)據(jù)可以看出:
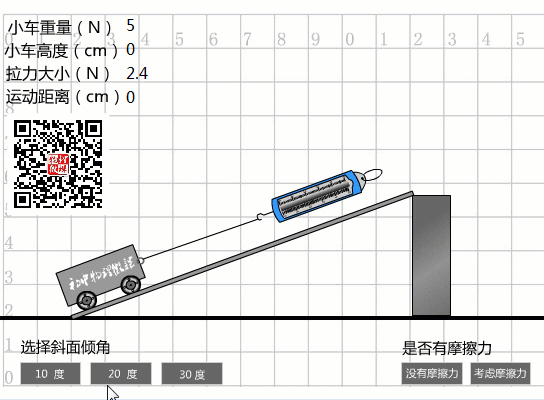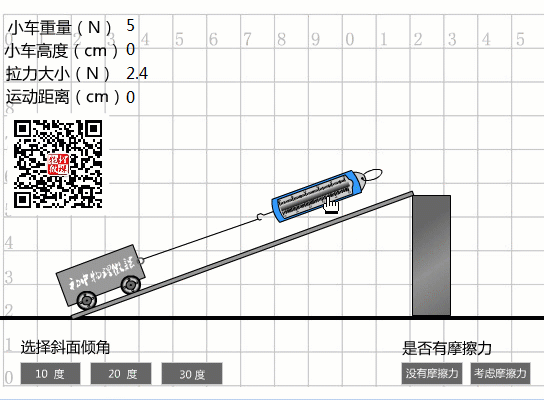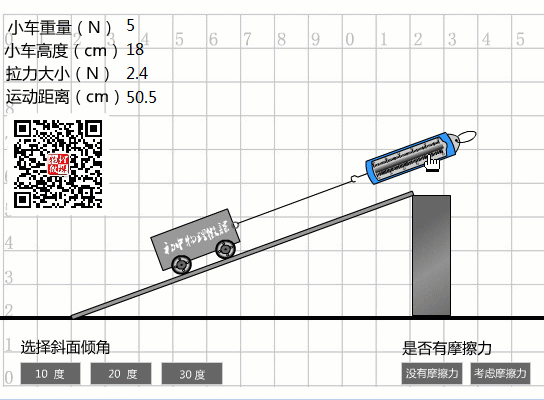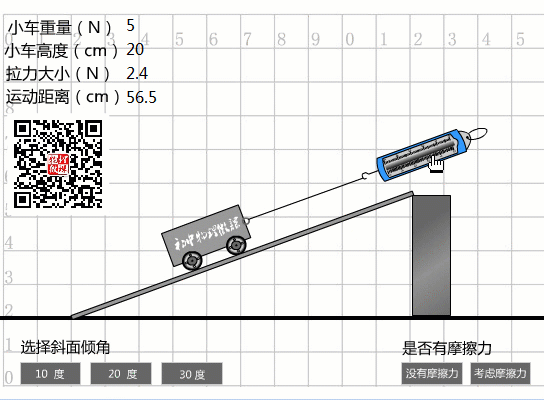
傾斜度為20度時(shí)的機(jī)械效率
我們實(shí)際做的事情:
W總計(jì)=Fs=2.4N×0.565m=1.356J。
機(jī)械效率:

η2=Whas/=1J/1.356J=73.7%。
當(dāng)選擇30度坡度時(shí),從圖中數(shù)據(jù)可以看出:
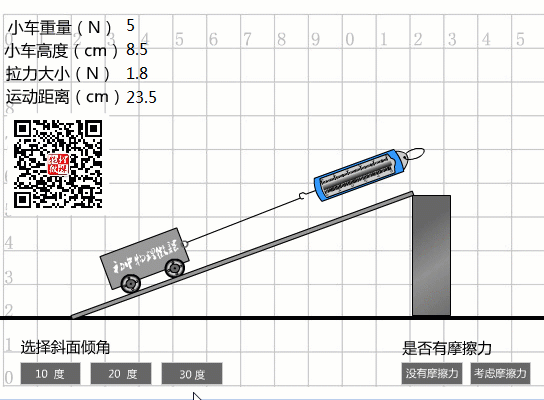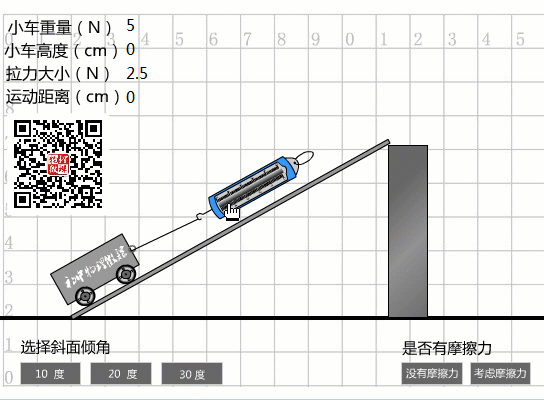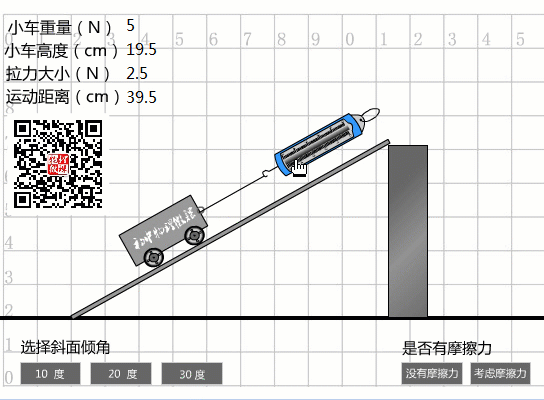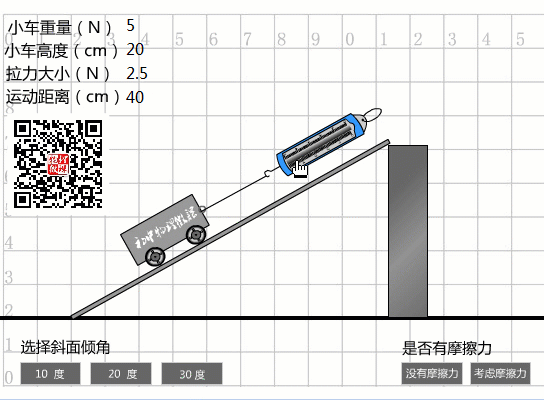
傾斜度為30度時(shí)的機(jī)械效率
我們實(shí)際做的事情:
W總計(jì)=Fs=3N×0.4m=1.2J。
機(jī)械效率:
eta3=Whas/=1J/1.2J=83.3%。
通過(guò)上述計(jì)算,從下表不難看出:斜坡的坡度越小,越省力,但機(jī)械效率較低。 如何解釋這一現(xiàn)象呢?
傾斜度(度)
拉力(牛)
數(shù)(%)
30
83.3
20
2.4
73.7
10
1.7
62.5
坡度越小,越容易省力。 這就是坡度的特點(diǎn)。 但同時(shí),坡度越小,汽車與坡度之間的正壓力就越大。 我們將在高中學(xué)習(xí)這個(gè)問(wèn)題。 當(dāng)然,壓力越大,摩擦力就越大。 。 那么,我們?yōu)榭朔Σ炼龅念~外工作就越多,那么機(jī)械效率就會(huì)相應(yīng)降低就不難理解了。
這個(gè)怎么樣? 你一看就明白了!
