

【答】分析:(1)已知推力的大小和推力方向移動的距離,根據公式W=Fs計算推力所做的總功;
(2)已知物體的重力和高度斜面上的機械效率,根據公式W=Gh計算推力所做的有用功,并根據公式η=
求斜面的機械效率;
(3)按照公式W量=W總計-W有用計算額外功。 推動物體過程中為克服摩擦力所做的功就是額外功。 根據公式W量=fs計算摩擦力;
斜面的機械效率與斜面的傾斜程度和斜面的摩擦力有關。
答:已知:推力F=500N,物體重力G=800N,斜坡長度s=3m,斜坡高度h=1.5m,
求: (1) 推力所做的總功W=?
(2) 機械效率 η =?
(3) ①摩擦力f=?
②如何提高機械效率?
解: (1) 推力所做的功:
W總計=Fs=500N×3m=1500J;
(2)克服重力所做的有用功:
W有用=Gh=800N×1.5m=1200J,
坡口機械效率:
n=
×100%=
×100%=80%;
(3) ①推力所做的額外功:W量=W總量-W有用=1500J-1200J=300J,
∵W 量=fs,
斜面對物體的摩擦力:
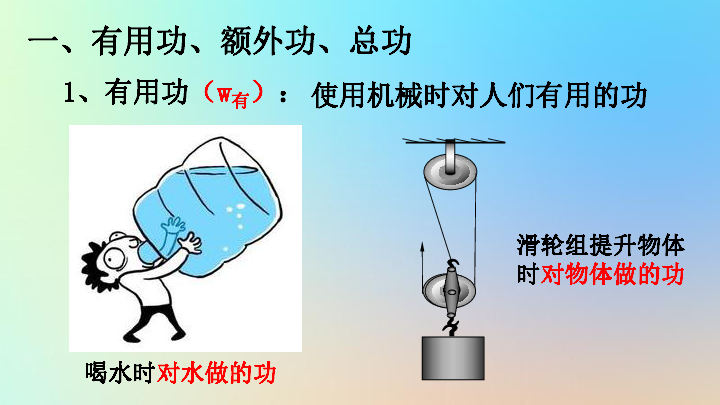
f=
=100N;
②要想提高斜面的機械效率,就必須在有用功不變的情況下盡量減少多余功。
方法一:當斜面的傾斜角度變大時,木箱對斜面的壓力逐漸變小。 當接觸面粗糙度不變時斜面上的機械效率,壓力越小,受到的滑動摩擦力越小,可以有效減少附加功。 .
方法二:減少斜面的摩擦力,可以減少額外的工作,提高其機械效率。
答:(1)推力所做的功為1500J;
(2)斜面機械效率為80%;
(3)①斜面對物體的摩擦力為100N;
②應采取的方法是:改用更光滑的坡口或加大坡口的傾斜角度。
點評:本題主要考查學生對有用功、總功、額外功和機械效率計算公式的理解和掌握,以及對機械效率增減方法的理解和掌握。 這是一個基本問題。