不請(qǐng)自來。
我回答這個(gè)問題只是為了整理和總結(jié)我所學(xué)的知識(shí)。
許多理論力學(xué)書籍的最后幾章都討論了虛功原理。 當(dāng)你學(xué)習(xí)理論力學(xué)時(shí)，你可能會(huì)發(fā)現(xiàn)虛功原理這一部分的“氣質(zhì)”與本書的其余部分有些不相容。 它更注重理論推導(dǎo)，而不是通過繪制力分析圖來獲得直觀的答案。 其實(shí)，這與經(jīng)典力學(xué)的發(fā)展歷史有關(guān)。 有興趣的同學(xué)可以在《力學(xué)史雜談》中搜索吳繼科寫的《經(jīng)典力學(xué)發(fā)展的兩條路徑》。 這里我們主要回答題主的問題：虛擬工作的原理是什么，它到底能做什么。
虛功原理的思想實(shí)際上起源于歐洲的伯努利家族，后來在拉格朗日的《分析力學(xué)》中得到了體現(xiàn)。 利用虛功原理可以推導(dǎo)出拉格朗日方程。 好了，那些看不懂的東西我們就不去管了，直接上圖吧。 如圖，這是最簡(jiǎn)單的彈簧，上面掛著一個(gè)小塊m。
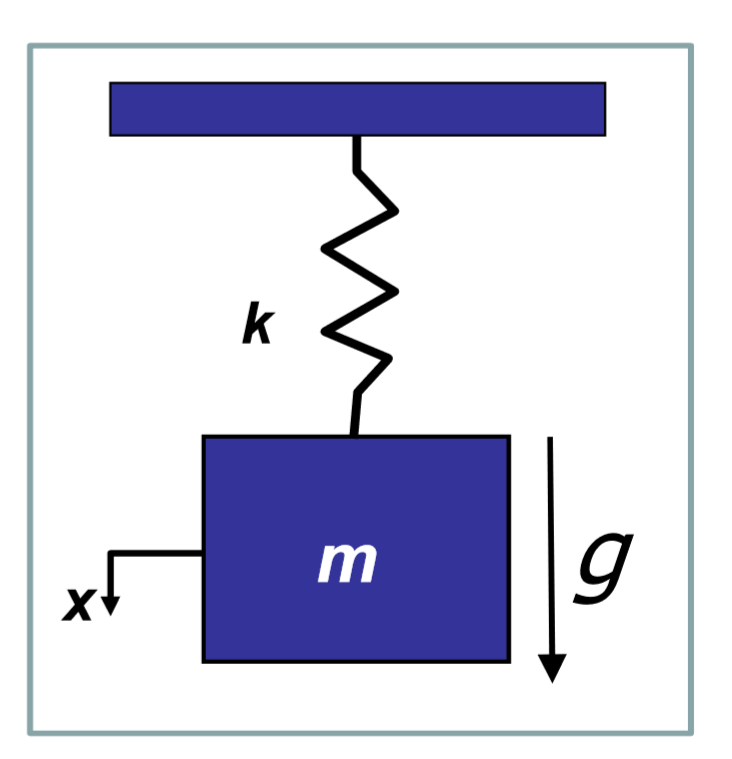
大公理工大學(xué)鐘萬(wàn)協(xié)院士在講座中通過引入彈簧的問題，可以清晰地解釋整個(gè)拉格朗日系統(tǒng)和哈密頓系統(tǒng)的主要思想。 虛擬工作原理是拉格朗日系統(tǒng)的墊腳石。 這里我也用彈簧的問題來解釋一下虛功的原理。 我保證只要學(xué)過高中物理，下面的推導(dǎo)就能理解。
在這個(gè)模型中，外力是彈簧上物體的重力，G=mg。 高中知識(shí)吧？ 那么當(dāng)加上這個(gè)外力時(shí)，彈簧就產(chǎn)生了變形，這個(gè)變形就相當(dāng)于外力對(duì)彈簧所做的功。 彈簧存儲(chǔ)了這項(xiàng)工作。 我們稱之為應(yīng)變能或彈性勢(shì)能。
V=frac{1}{2} kx^{2}
這個(gè)1/2從哪里來？ 這里的彈性勢(shì)能可以理解為彈簧內(nèi)力（即彈力F=kx）對(duì)彈簧變形所做的負(fù)功的積分。即可以寫為
V=frac{1}{2} F x
彈簧的內(nèi)力為F=kx，變形從0逐漸增大到x時(shí)所做的功。
到目前為止功等于什么，這都是高中知識(shí)。 虛功原理是指當(dāng)系統(tǒng)處于平衡狀態(tài)時(shí)，如果給該系統(tǒng)一個(gè)虛位移δx，則外力對(duì)虛位移所做的功等于內(nèi)力對(duì)系統(tǒng)所做的功。虛擬位移。 我們來驗(yàn)證一下：
外力G=mg虛位移所做的功
W_{1} =Gdelta x
內(nèi)力 F = kx 對(duì)虛擬位移所做的功
W_{2} =Fdelta x
將兩者相等，并消除左右虛擬位移，我們發(fā)現(xiàn)什么？ kx=mg，求x，即系統(tǒng)處于平衡狀態(tài)時(shí)對(duì)應(yīng)的x。
這里，彈簧的內(nèi)力對(duì)虛擬位移所做的功實(shí)際上是前一個(gè)彈簧的勢(shì)能的一階變化。
這道題簡(jiǎn)單到高中生一看就知道結(jié)果。 看起來，用虛功原理和力量平衡的原理來解決，并沒有什么區(qū)別。
但當(dāng)問題從彈簧變?yōu)楹?jiǎn)支梁時(shí)，情況就不同了。 雖然事實(shí)上簡(jiǎn)支梁也是線彈性體。 如果你愿意的話，你當(dāng)然可以把梁的反力方程中除了x之外的所有項(xiàng)放在一起，并設(shè)置為k，這樣問題就和彈簧的問題一模一樣了。
—————————————————
當(dāng)你的系統(tǒng)不再是一個(gè)簡(jiǎn)單的彈簧小塊，而是變成一維梁、二維板、三維混凝土?xí)r，剛才的虛功原理會(huì)發(fā)生什么變化呢？
彈性體受力后會(huì)發(fā)生一定程度的變形功等于什么，最終達(dá)到平衡狀態(tài)。 當(dāng)平衡時(shí)滿足邊界條件時(shí)（對(duì)于梁來說是鉸接節(jié)點(diǎn)或剛體節(jié)點(diǎn)物理資源網(wǎng)，對(duì)于板來說是中間支撐邊或夾層支撐邊的條件），空間彈性體的位移場(chǎng)可以為用x、y、z、v、w這三個(gè)函數(shù)u來表示。
由此，可以建立彈性體的應(yīng)變能函數(shù)U——獨(dú)立函數(shù)為u、v、w，函數(shù)值為彈性體的應(yīng)變能。 這里的虛功原理也稱為虛位移原理：給定一個(gè)虛位移δx，所有外力對(duì)該虛位移所做的功δW等于內(nèi)力所做的功δU關(guān)于虛擬位移。
δU=δW
外部虛功等于內(nèi)部虛功。 這個(gè)方程與上面的彈簧問題相似嗎？
通過求解這個(gè)方程，我們得到了彈性體的真實(shí)位移場(chǎng)，它對(duì)應(yīng)于上面彈簧問題中的x。
進(jìn)一步，我們假設(shè)彈性體的應(yīng)變勢(shì)能為U，外力勢(shì)能為V（這里V的絕對(duì)值為負(fù)）。 這里，U和V都是位移u、v、w的函數(shù)。 各種公式介紹了變分法。 書上都有，這里就不提了。 彈性體的總勢(shì)能為PI=U+V。
求解時(shí)，首先建立滿足位移邊界條件的位移場(chǎng)函數(shù)的形式。 它可以是多項(xiàng)式形式或三角函數(shù)形式。 只要滿足邊界條件，任何一種方法都有效。 該位移場(chǎng)函數(shù)中可能存在許多未定系數(shù)，如C1、C2、C3等。 無論取多少個(gè)系數(shù)，該位移場(chǎng)都能滿足位移邊界條件。 那么哪個(gè)才是真正的位移場(chǎng)呢？
最小勢(shì)能原理告訴我們，真實(shí)的位移場(chǎng)使總勢(shì)能泛函最小，即PI剛才的變化為零。
δPI=δU+δV=0
注意，我剛才說V的絕對(duì)值為負(fù)數(shù)。 到了等號(hào)的另一邊，就變成剛才的虛功原理了。
δU=δW
因此，最小勢(shì)能原理是虛功原理的等價(jià)形式。
您可以說，在所有可能的位移中，處于平衡狀態(tài)的位移使系統(tǒng)的總勢(shì)能最小化。 等效的說法是，在平衡位置，外力的虛功等于內(nèi)力的虛功。
至于最小勢(shì)能原理和變分法有什么用，請(qǐng)關(guān)注我的另一個(gè)回答：