

隔離和整體治療
1.隔離方法所謂隔離方法,就是把某些研究對象或物理問題的某些過程或狀態(tài)從系統(tǒng)或整個(gè)過程中孤立出來進(jìn)行研究的方法。
隔離有兩種類型:
(1)對象隔離:為了找到與某個(gè)對象相關(guān)的期望量和已知量之間的關(guān)系,將一個(gè)對象從系統(tǒng)中隔離出來。
(2)過程隔離:物體往往要參與幾個(gè)運(yùn)動過程,為了解決某一過程所涉及的物理量,需要把這一過程從整個(gè)過程中隔離出來。
2、所謂整體方法,是指研究物理問題的整個(gè)系統(tǒng)或過程的方法,這也包括兩種情況:
(1)把物體系統(tǒng)作為一個(gè)整體來研究:當(dāng)所要研究的物理量不涉及系統(tǒng)中某個(gè)物體的力和運(yùn)動時(shí)貝語網(wǎng)校,常采用這種方法。
(2)整體研究整個(gè)運(yùn)動過程:常用于所要求的物理量只涉及整個(gè)運(yùn)動過程的情況。
另外,為了幫助高中生提高成績,我和清華北大的學(xué)長學(xué)姐一起整理了不少高中學(xué)習(xí)資料,篇幅有限,有興趣的朋友可以關(guān)注我的公眾號,隨時(shí)更新高中九大科目的學(xué)習(xí)資料,只要努力,成績提升很容易。
具體方法:微信-右上角加號-添加好友-公眾號-進(jìn)入公眾號【高中生學(xué)習(xí)資料庫】,關(guān)注并發(fā)送“6767”即可收到全科模擬試題及相關(guān)資料,幫助你考上更好的大學(xué)
等效方法
等效方法是物理學(xué)中的一種基本思維方法,其實(shí)質(zhì)是在保證效果相同的條件下,把復(fù)雜的情況或過程轉(zhuǎn)化為簡單的情況或過程。
1. 力的等價(jià)性
合力與分力是等效的,通過把作用于物體上的多個(gè)恒定力等效為一個(gè)力,可以將復(fù)雜的物理模型轉(zhuǎn)化為相對簡單的物理模型,大大降低解決問題的難度。
2.運(yùn)動的等價(jià)性
由于合成運(yùn)動與分運(yùn)動等效,因此,拋射運(yùn)動可以看作是水平方向的勻速直線運(yùn)動與豎直方向的自由落體運(yùn)動的合成運(yùn)動。
“舟渡江”中小船的運(yùn)動,可以看作是沿水流方向的勻速直線運(yùn)動與垂直于河岸的勻速直線運(yùn)動的合成運(yùn)動。當(dāng)計(jì)算大小不變,方向變化的阻力所作的功,如空氣阻力所作的功時(shí),物體做直線運(yùn)動時(shí),可適用公式W=fS,只不過公式中的S是距離而不是位移。不管物體運(yùn)動方向如何變化,都可以等效為在恒定力f作用下的單向直線運(yùn)動。
3.物理過程的等效性
如果一個(gè)研究對象從相同的初狀態(tài)出發(fā),經(jīng)過兩個(gè)不同的過程,最后達(dá)到相同的終狀態(tài),則這兩個(gè)過程是等價(jià)的。
4. 模型等價(jià)性

等價(jià)性是指互相替代所產(chǎn)生的效果是一樣的,利用等價(jià)性方法,不僅可以把非理想模型變成理想模型,把復(fù)雜問題變成簡單問題,而且可以將感性認(rèn)識上升為理性認(rèn)識,把一般理性認(rèn)識升華為更深的層次。
在解決問題的過程中,我們用到的最常見、典型的物理模型并不多,比如碰撞模型、人船模型、子彈射擊木塊模型、衛(wèi)星模型、彈簧振子模型等等。
5.實(shí)驗(yàn)原理的等效性
在高中物理力學(xué)實(shí)驗(yàn)中,幾乎可以說,沒有等效思想,就“無法前行”。
在《力的測量》中,基于平衡條件,用等效的觀點(diǎn),我們所要測量的力,相當(dāng)于彈簧中的彈力,物體所受的重力,相當(dāng)于平衡狀態(tài)下物體所受支撐面所受的拉力。
在“驗(yàn)證平行四邊形力的定律”這個(gè)實(shí)驗(yàn)中,充分利用了等效概念,用一個(gè)力產(chǎn)生的效果等同于用兩個(gè)力產(chǎn)生的效果——把橡皮筋拉長到某一位置,這樣就得到,這個(gè)力可以等效于那兩個(gè)力。
等效性在“驗(yàn)證動量守恒定律”實(shí)驗(yàn)中的應(yīng)用已經(jīng)發(fā)揮到了極致,由于小球從同一高度出發(fā),做水平運(yùn)動,它們在空中的飛行時(shí)間是相同的,以飛行時(shí)間為單位時(shí)間,我們可以用水平距離來表示水平速度,也就是把水平速度等效地用水平距離代替。
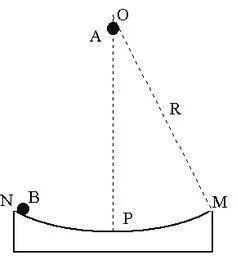
【例1:】如圖所示,半徑為R的光滑圓弧槽∠POM

【例二:】如圖所示,兩個(gè)底部面積S相同的圓桶放在同一平面上,桶內(nèi)盛滿水,水面高度分別為h1、h2。已知水的密度為ρ。現(xiàn)將兩個(gè)桶連接起來,打開桶的閥門K,直至兩個(gè)桶的水位相等。在此過程中,水的重力勢能如何變化?變化量為多少?水的動能如何變化?變化量為多少(忽略阻力)
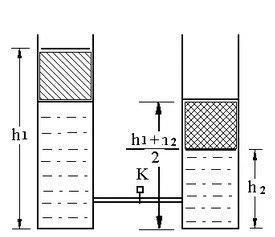
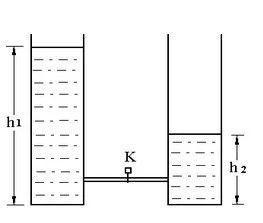
【解析】本題中,閥門K打開后,左邊桶里的水逐漸流向右邊桶,直至兩桶水位相等,這個(gè)過程我們不需要深究,如果觀察起始狀態(tài)和終止?fàn)顟B(tài)(比如整個(gè)過程就相當(dāng)于左邊桶里高度(h1+h2)/2以上的部分,即陰影部分,移動到右邊桶里的陰影部分。
這部分水的質(zhì)量為m=ρS(h1+h2)/2;重心下落的高度為h=(h1-h2)/2;
因此,忽略阻力,水的重力勢能減少ρgS(h12-h22)/4。水的動能增加ρgS(h12-h22)/4。
極值法
描述過程的物理量受物理規(guī)律或條件的限制,其值只能在一定的范圍內(nèi)才能滿足實(shí)際的物理問題,在這個(gè)范圍內(nèi),物理量可能存在最大值、最小值或者決定其范圍的邊界值等一些特殊值。
解決極值問題有以下幾種方法:

極端思維

極限思維方法是一種比較直觀、簡便的科學(xué)方法高中物理的四個(gè)層次是什么,在物理學(xué)研究中,經(jīng)常用來解決某些不能直接驗(yàn)證的實(shí)驗(yàn)和規(guī)律,例如伽利略在研究一個(gè)球沿斜面滾下的運(yùn)動時(shí),把第二個(gè)斜面向外推到它的極限——水平面;
在物理練習(xí)中,有些題目涉及到比較復(fù)雜的物理過程,這些物理過程屬于一個(gè)較大的物理過程,這個(gè)復(fù)雜的物理過程需要分解成若干個(gè)小的過程,這些小過程的變化比較單一,因此運(yùn)用極限思維方法,選取整個(gè)過程的兩個(gè)端點(diǎn)和中間的奇異點(diǎn)進(jìn)行分析,結(jié)果就包含了所要討論的物理過程,使得解題過程簡單直觀。
【例】如下圖所示,上方固定一輕彈簧,下方懸掛一質(zhì)量為m0的平板,平板內(nèi)有一質(zhì)量為m的物體,當(dāng)平板靜止時(shí),彈簧的長度比其自然長度伸長l。現(xiàn)在將平板向下拉,使彈簧伸長Δl后停止,然后松手。假設(shè)彈簧始終在彈性極限以內(nèi),則剛松手時(shí)平板對物體的支撐力等于( )
【解析】設(shè)給定條件下Δl=0,即圓盤沒有被拉下,如果放手,彈簧長度不變,圓盤保持靜止,圓盤對物體的支撐力應(yīng)為mg。
將Δl=0代入四個(gè)備選答案中,只有答案A能得到mg,所以只有答案A正確,本題應(yīng)選A。
圖像法
使用圖形解決物理問題的步驟
1、清楚了解縱、橫坐標(biāo)所表示的物理量;
2、看圖形本身,找出兩個(gè)物理量的變化趨勢,分析具體的物理過程;
3、看兩個(gè)相關(guān)量的變化范圍和所給的有關(guān)條件,明確圖形與坐標(biāo)軸交點(diǎn)、圖形斜率、圖形與坐標(biāo)軸所圍成的“面積”的物理意義。
【例】(2012國家新課程標(biāo)準(zhǔn))如圖所示,在一塊木板與一面垂直的墻面之間放置一個(gè)小球,設(shè)墻面對小球的壓力為N1,小球?qū)δ景宓膲毫镹2。以小球與墻面連線所成的水平線為軸,將木板從圖示位置緩慢轉(zhuǎn)到水平位置。忽略摩擦力,此過程中( )。
A.N1 總是減少,N2 總是增加 B.N1 總是減少,N2 總是減少
C.N1先增大后減小,N2始終減小;D.N1先增大后減小,N2先減小后增大。
【解析】本題考查物體的動態(tài)平衡,由對小球受力的分析可知,N1、N2的合力為一個(gè)常數(shù),且等于重力的反方向,畫出圖形,從圖中可知,當(dāng)盤子緩慢旋轉(zhuǎn)時(shí),N1、N2的合力的方向如圖所示發(fā)生變化,但合力保持不變,故答案為B。
臨界條件法
物理系統(tǒng)由于某種原因而發(fā)生突變時(shí)的狀態(tài)稱為臨界狀態(tài)。臨界狀態(tài)可以理解為“剛出現(xiàn)”或“剛不出現(xiàn)”兩種狀態(tài)。突變過程是一個(gè)由量變到質(zhì)變的過程。在臨界狀態(tài)前后,系統(tǒng)遵循不同的規(guī)律,按照不同的規(guī)律運(yùn)動和變化。
如光學(xué)中折射的“臨界角”、超導(dǎo)中的“臨界溫度”、核反應(yīng)中的“臨界體積”、光電效應(yīng)中的極限頻率、靜摩擦中的最大靜摩擦力等等。
在中學(xué)物理中,這種表述明確的臨界值是容易理解和掌握的,但在高考題目中,臨界值往往表述不清,必須運(yùn)用所學(xué)的知識去分析臨界條件,找出臨界值。很多物理問題都涉及到臨界問題,分析臨界問題的關(guān)鍵就是找出臨界狀態(tài)的條件。
解決關(guān)鍵問題通常有兩種基本方法:
1.以定理、定律為基礎(chǔ)高中物理的四個(gè)層次是什么,首先找出所研究問題的一般規(guī)律和一般解,然后分析、討論它的特殊規(guī)律和特殊解。
2.直接分析討論臨界狀態(tài)及對應(yīng)的臨界值,找出研究問題的規(guī)律和解決辦法。