這個專題的核心要點在于“分段剖析運動狀態(tài)”,依據(jù)交變電場所具備的周期性,把運動劃分成多個“恒力作用的階段”,每一個階段都拿來類比“勻強電場里的運動”(直線或者類平拋),然后借助周期性對整個過程進行整合 。


一、核心前提:明確交變電場的“表達式與周期”
解題第一步是理清電場的變化規(guī)律,常見兩種形式:
隨時間變化的電壓(或者場強)的影像:像是方波、正弦波、鋸齒波(關鍵在于找尋“場強保持穩(wěn)定的時間段”,比如方波的每一個周期里面,前t0時間E等于E1,之后的t0時間E等于E2)。
如呀,存在著文字所描述的類似這樣的周期性,也就是,電場方向呢,每T時間它就會反向一次,并且呀,其大小始終是為E 。
二、兩大典型運動模型
1. 沿電場方向的直線運動(最常見)
粒子剛開始的速度和電場的方向呈現(xiàn)共線狀態(tài),此共線狀態(tài)存在同向或者反向兩種情況,在每一個周期之內(nèi),粒子受到的電場力保持恒定,或者是受到方向相反的恒定電場力作用,粒子的運動過程被劃分成加速階段以及減速階段,其中的關鍵要點是,運用運動學公式或者動量定理,針對每一段的速度以及位移展開分析高中物理電場問題題目,之后再依據(jù)周期性來判斷粒子最終的運動趨勢。
常見場景與分析方法:


2. 垂直電場方向的類平拋運動(含周期性偏轉)
粒子開始時的速度跟電場的方向是相互垂直的,電場呈現(xiàn)周期性的變化致使“在豎直方向(也就是電場方向)上的加速度出現(xiàn)周期性的變化”,關鍵核心在于“在水平方向是做勻速運動,而在豎直方向是進行分段的勻變速運動”,需要留意“當電場方向反向的時候起步網(wǎng)校,在豎直方向上的運動狀態(tài)有可能從‘加速’轉變?yōu)椤疁p速’,甚至還會出現(xiàn)反向加速的情況” 。
示例:
攜帶正電的粒子,以水平的初速度v_0,進入一個區(qū)域,這個區(qū)域水平方向是勻速的,豎直方向電場每隔T時間進行反向,且大小恒定為E 。
分析:

三、解題關鍵技巧
核心為“分段法”,不論何種運動,都要依據(jù)“電場恒定的時間段”來拆分運動,將每一段看作是“勻強電場中的恒力運動”,防止直接運用“周期性公式”生硬套用。
2. 優(yōu)先畫“運動過程圖”和“v-t圖像”:
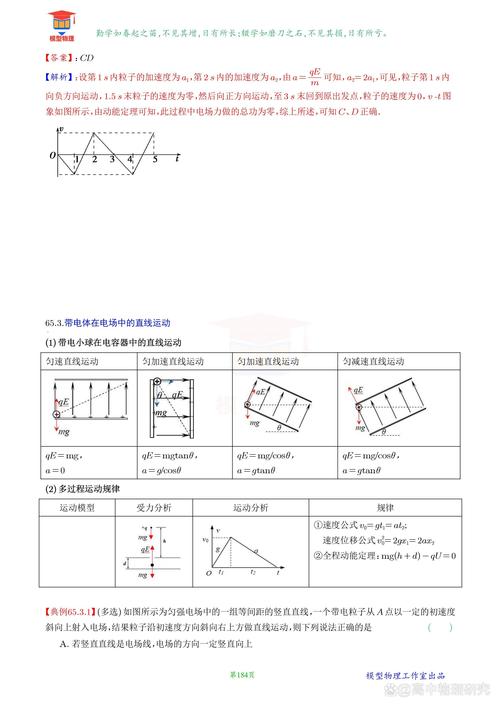
v - t圖像能夠直觀地呈現(xiàn)出速度怎樣發(fā)生變化,加速度如何產(chǎn)生變化(通過斜率體現(xiàn)),位移又是怎樣的情況(借助面積表示),特別適宜用于分析速度是不是出現(xiàn)了反向的情況,位移是不是在不斷累加 。
3. 判斷“粒子是否穿出電場”:
若粒子于電場里的運動時間,通過水平位移L等于v_0 t進行計算得出,且該運動時間小于交變電場周期,那么僅需對“一個不完整周期內(nèi)的運動”予以分析,而無需考慮其周期性,。
倘若運動的時間比周期更長,那就需要先去剖析一番“一個 周期之內(nèi)的位移以及速度的變化情況”,而后再去判定后續(xù)周期的運動走向(像是是否能夠持續(xù)加速、做往復運動之類的)。
4. 巧妙運用“動量定理”來使計算得到簡化:倘若涉及到“多段運動的總的速度發(fā)生變化”這種情況,那么可以運用動量定理(合外力的沖量等于動量的變化,也就是I總等于mv末減去mv初),以此來避免進行分段計算速度時所呈現(xiàn)出的繁雜。
四、易錯點提醒
將“電場方向與粒子電性的關系”予以忽略高中物理電場問題題目,正電荷所受的力的方向跟電場方向是相同的,而負電荷所受的力的方向與電場方向相反,要做的事情是先把每一段的加速度方向確定下來。
把“位移周期性”錯誤地當作“速度周期性”,在一些場景里,位移按照周期進行累加,像粒子持續(xù)朝著某一個方向運動那樣,然而速度有可能周期性地變?yōu)榱悖热缦燃铀伲贉p速到零,接著反向加速,然后反向減速到零 。
未對“臨界狀態(tài)”加以考量,像粒子于穿出電場之前,其速度已然減至零且朝著相反方向運動,這種情況下需要去計算“速度為零的那個時刻”,以此來判定是否真的穿出了電場。
