貢獻(xiàn)者: ; addis
電場(chǎng)高斯定律相關(guān)的預(yù)備知識(shí),磁場(chǎng)高斯定律相關(guān)的預(yù)備知識(shí),靜磁學(xué)范疇的安培環(huán)路定律相關(guān)的預(yù)備知識(shí),。
文中,我們歸納一些靜電場(chǎng)與靜磁場(chǎng)的基本。這兒所說“靜”,指系統(tǒng)狀態(tài)不隨時(shí)間改變,像電荷、電流、電場(chǎng)等強(qiáng)度與分布皆恒定。留意,這兒“靜”與“靜止”含義不完全一樣,不意味著沒電荷流動(dòng)(電流),僅表明電荷流動(dòng)速度均勻,即所謂“穩(wěn)恒電流”。
1. 電荷、電流與電荷守恒電荷
啥是電荷呢,依據(jù)富有深意表述來講,電荷是粒子跟電磁場(chǎng)交互作用的強(qiáng)度,然而,對(duì)初學(xué)者而言,你只需曉得電荷跟質(zhì)量一樣,同樣是粒子或物質(zhì)的一種性質(zhì),之所以引入電荷這一概念,是由于人們發(fā)覺物質(zhì)間除了有起源于質(zhì)量的引力交互作用之外,還存在另一種交互作用,其強(qiáng)度跟質(zhì)量沒有關(guān)聯(lián)、但跟物質(zhì)的另一種性質(zhì)有關(guān)聯(lián),人們把這種性質(zhì)稱作電荷,這種交互稱作靜電力 。
當(dāng)電荷呈現(xiàn)離散分布的狀況時(shí),比如說,我們所熟知的有著對(duì)應(yīng)“質(zhì)點(diǎn)”的點(diǎn)電荷模型,此時(shí),我們能夠具體描述每一個(gè)點(diǎn)電荷所攜帶的電荷量$q_i$;而當(dāng)電荷處于連續(xù)分布的情形時(shí),例如,存在一個(gè)處處都帶電的物體,有著對(duì)應(yīng)“剛體”,此刻,我們更傾向于運(yùn)用電荷密度,也就是單位體積的電荷量$rho = frac{ldp5vth{q}}{jj5rd5d{V}} $。
電流
當(dāng)電荷,大量的電荷,朝著一定方向,做具有指向特點(diǎn)的運(yùn)動(dòng),開始行動(dòng)起來的時(shí)候,就能產(chǎn)生電流。這個(gè)電流呢,可以通過電流強(qiáng)度$I$以及電流密度${{j}}$來進(jìn)行表述:
表1:電流強(qiáng)度與電流密度
電流強(qiáng)度 $I$:“單位時(shí)間通過截面的電荷量”
不太明確你給出的這個(gè)式子具體要表達(dá)什么意思及具體改寫需求準(zhǔn)確改寫呢。這個(gè)式子似乎按正常數(shù)學(xué)表述應(yīng)該是。
反映電流分布疏密程度的物理量電流密度,它指的是,在單位時(shí)間范疇以內(nèi)呀,又在單位面積前提下呢,所通過的電荷量啦。
$I$等于沿閉合路徑環(huán)繞一周的,對(duì)這樣一種所謂的“{{j}}”與“{xldnp5r}}{{{S}} }”做點(diǎn)乘運(yùn)算的結(jié)果~ 而“{{j}}”等于,對(duì)“$I$”關(guān)于“$S_perp$”求微分后,再乘以“$hat n$”~ 還有,“{{j}}”等于,“$n$”乘以“$e$”再乘以“{{v}}”~ 這里面,“$n$”是,那種作為電荷載體的載流子的體積數(shù)密度,“$e$”是每一個(gè)載流子所帶的電荷量,“{{v}}”是載流子的速度。
電荷守恒
質(zhì)量相同的情況下,電荷是保持守恒狀態(tài)的沒錯(cuò)。這意味什么呢,就是假如有那么一個(gè)地段有電荷向外流出了(也就是產(chǎn)生電流這種情況),那么在這個(gè)地段內(nèi)的電荷量就會(huì)照著比例相應(yīng)地減少。閉合積分符號(hào)下電流密度 ({{j}}) 與面元 (lzbv57h{{{s}}}overd ot) 整合,結(jié)果等于負(fù)的對(duì)時(shí)間 (t) 求導(dǎo),該導(dǎo)數(shù)表達(dá)式為對(duì)電荷密度 (rho) 在體積 (V) 上積分,且電荷密度 (rho) 等于電荷量 (q) 對(duì)體積 (V) 求導(dǎo),還有電流和關(guān)系中各項(xiàng) (I_i) 求和,其和等于負(fù)的電荷量 (q) 對(duì)時(shí)間 (t) 求導(dǎo),這里規(guī)定 (I>0) 時(shí)表示流出該區(qū)域的電流是流入的電流的相反狀態(tài),否則就是流入的電流 。上述式子呈現(xiàn)出的微分形式是,存在這樣一個(gè)等式,即▽·j這兒,加上ρ之上除以t,其結(jié)果等于0 。在處于靜場(chǎng)的狀況之下,空間里面的電荷密度以及電流密度,它們是都不太會(huì)隨著時(shí)間而發(fā)生何種變化的,鑒于此,就會(huì)有▽·j等于0 ,并且會(huì)有∑iIi等于0這一情況 。這個(gè)所得出的結(jié)論還被稱呼為基爾霍夫第一定律。
2. 靜電場(chǎng)與靜磁場(chǎng)
圖1,電荷于一個(gè)截面上產(chǎn)生電場(chǎng)的示意圖,電流則在該截面上產(chǎn)生磁場(chǎng)的示意圖,CC 0 。
眾人皆知,電荷會(huì)在其周圍產(chǎn)生電場(chǎng),電流會(huì)在其所及之處產(chǎn)生磁場(chǎng)。如下的表格呈現(xiàn)出電荷、電流跟它們所生成的電場(chǎng)、磁場(chǎng)之間的關(guān)聯(lián):
表2:靜電場(chǎng)與靜磁場(chǎng)
電場(chǎng) $ {{E}} $
磁場(chǎng) $ {{B}} $
場(chǎng)源
電荷 $q$
電流 (運(yùn)動(dòng)的電荷) $I$
場(chǎng)源產(chǎn)生的場(chǎng)

5bv7vzx{{E}}({{r}})等于四π分之一與(frac57bldr7{q})除以(R^2)再乘以({{hat R}})的乘積,不大嚴(yán)格地講,b5rtn7r{{E}}這么得出的結(jié)果其是由單個(gè)小電荷p5z5d7h{q}所生成的在空間中電場(chǎng)的該些物理狀態(tài)變化所組成 。 且rtvfflj{{E}}是電場(chǎng) , 是由單個(gè)小電荷jh5xzp7{q}而產(chǎn)生形成的那種電場(chǎng) 。 又n5hzrft{{E}}是由那單個(gè)小在帶電方面呈現(xiàn)微小量狀態(tài)的電荷jfxj7z9{q}這一因素致使產(chǎn)生的電場(chǎng) 。 還dh7bnlz{{E}}是因單個(gè)小電荷llv57th{q}處于帶電呈現(xiàn)微小表現(xiàn)的狀態(tài)從而造成產(chǎn)生的電場(chǎng)情況 。 需注意的是,你提供。
其中,(57zbb7b{{{B}}})對(duì)({{r}})的表達(dá)式為,(μ)帶有下標(biāo)(0),除以(4)再乘以圓周率,乘以(I)與(j3tlntz{{{r}}'})的乘積,然后除以(R)的平方,而此(R)上帶有符號(hào)(hat{{{R}}})之后,這整個(gè)式子就是畢奧—薩伐爾定律,并且請(qǐng)注意,這里的(rtdxxlh{{{B}}})乃是由一段一小段的電流(I)與(lnhjdb5{{{r}}'})所生成產(chǎn)生的磁場(chǎng) 。
線性疊加原理
在表達(dá)式里,存在等式({{E}} ( {{r}} ))的值,其等同為積分(int ,dfphr5n{ {{E}} ),而這個(gè)積分呢,又跟(frac{1}{4 pi } int frac{ ,x5fhbhn{q} }{R^2} {{hat R}} ~)相等 ,因?yàn)閷?duì)應(yīng)的方程具備線性特征,所以當(dāng)空間里存在多個(gè)電荷時(shí),這些電荷所引發(fā)的總電場(chǎng)可表示為各個(gè)電荷分別產(chǎn)生的電場(chǎng)的總和 。
第一個(gè)大左花括號(hào)括著的(B),括號(hào)里是大左花括號(hào)括著的(r),等于線積分大右花括號(hào)(d),大右花括號(hào)里是兩個(gè)大左花括號(hào)括著的(B),等于(frac{mu_0}{4pi}),乘以積分里(I),乘以大右花括號(hào)(d),大右花括號(hào)里又出現(xiàn)兩個(gè)大左花括號(hào)括著的(r)”,再叉乘單位向量尖大右花括號(hào)括著字母(R。
散度方程
那圍繞著的,對(duì)這樣的一個(gè)集合矢量(E)做點(diǎn)乘,且是對(duì)那樣的一個(gè)集合曲面元(ds)進(jìn)行積分,其結(jié)果等于,分之一,對(duì)這樣的一個(gè)密度(rho)在那樣的一個(gè)體積元(dV)上進(jìn)行積分,又等于,分之一,電荷量(Q) , 那散度算符作用于這樣一來的集合矢量(E) ,其結(jié)果等于,分之一,密度(rho) , 這就是電場(chǎng)的高斯定律 。
閉合曲線積分,磁場(chǎng)強(qiáng)度矢量與微小面積元矢量點(diǎn)乘的環(huán)量等于零,旋度算符與磁場(chǎng)強(qiáng)度矢量做點(diǎn)乘結(jié)果為零,這就是磁場(chǎng)的高斯定律。
旋度方程
環(huán)繞積分一個(gè)由雙花括號(hào)括起來的磁場(chǎng)矢量與一個(gè)由花括號(hào)括起來的線元矢量相乘的表達(dá)式,其結(jié)果等于磁導(dǎo)率常數(shù)乘以一個(gè)由雙花括號(hào)括起來的電流密度矢量與一個(gè)由花括號(hào)括起來的面積元矢量相乘的積分,此積分又等于磁導(dǎo)率常數(shù)乘以電流,一個(gè)由 nabla 算符與后面跟著叉乘符號(hào)以及一個(gè)由雙花括號(hào)括起來的磁場(chǎng)矢量組成的表達(dá)式等于磁導(dǎo)率常數(shù)乘以一個(gè)由雙花括號(hào)括起來的電流密度矢量,這就是靜磁場(chǎng)的環(huán)路定理(專業(yè)術(shù)語:安培環(huán)路定律)。
其中,{{r}}是場(chǎng)點(diǎn),{{r}}'是場(chǎng)源位置,{{R}}等于{{r}}減去{{r}}'是從場(chǎng)源處指向場(chǎng)點(diǎn)的矢量,{{\hat R}}是與之對(duì)應(yīng)的單位矢量。,$\mu_0$分別是“真空介電常數(shù)”和“真空磁導(dǎo)率”(按其等表述,這兩個(gè)術(shù)語的稱謂存在誤導(dǎo)性,只需清楚它們是常數(shù)即可)。
為啥有了好看的“場(chǎng)源產(chǎn)生的場(chǎng)”,還得要(微分形式的)那既包含散開程度指示又包含旋轉(zhuǎn)程度指示的方程呢?雖說二者能夠相互“得來結(jié)果”,然而那既包含散開程度指示又包含旋轉(zhuǎn)程度指示的方程還是有著(潛藏的、理論層面上的)好處:
3. 電(標(biāo))勢(shì)與磁矢勢(shì)
從數(shù)學(xué)以及物理意義方面展開考量,那樣我們能夠去引入勢(shì)的概念。有時(shí)候運(yùn)用勢(shì)的概念,會(huì)展現(xiàn)出比場(chǎng)更加簡(jiǎn)潔,且比場(chǎng)更為深刻的特點(diǎn)。
表3:電(標(biāo))勢(shì)與磁矢勢(shì)
電場(chǎng) $ {{E}} $
磁場(chǎng) $ {{B}} $
$$~$$ 電勢(shì),標(biāo)量函數(shù)
$$ {{A}} ~$$ 磁矢勢(shì),矢量函數(shù)
勢(shì)與場(chǎng)
先看第一個(gè)式子:這個(gè)式子表示,有一個(gè)等于負(fù)的梯度的量,它與某個(gè)東西相關(guān),這個(gè)東西是什么呢,它其實(shí)是對(duì)從零勢(shì)參考點(diǎn)到當(dāng)前位置的路徑進(jìn)行積分時(shí),與之前提到某個(gè)等于負(fù)的梯度的另一量做點(diǎn)乘運(yùn)算從而得到的結(jié)果里的那個(gè)積分下限所對(duì)應(yīng)的位置相關(guān)的一個(gè)量,這里零勢(shì)參考點(diǎn)一般選取無窮遠(yuǎn)處勢(shì)為0,具體參考下文的“規(guī)范”,這里的積分下限所在位置一般就是零勢(shì)參考點(diǎn),也就是通常選取無窮遠(yuǎn)處勢(shì)為0的那個(gè)點(diǎn),這里所說的零勢(shì)參考點(diǎn),在具體參考下文的“規(guī)范”時(shí),其選取一般是無窮遠(yuǎn)處勢(shì)為0 。再看右邊的式子:它是從零勢(shì)參考點(diǎn)到當(dāng)前位置的積分,積分的被積函數(shù)是之前提到那個(gè)等于負(fù)的梯度的量與路徑微元做點(diǎn)乘運(yùn)算的結(jié)果,這里零勢(shì)參考點(diǎn)一般選取無窮遠(yuǎn)處勢(shì)為0,具體參考下文的“規(guī)范” 。
大括號(hào)括起來的B等于,nabla叉乘,大括號(hào)括起來的A 。
勢(shì)的任意性,“規(guī)范”
$$ += ~$$ $$ 是常數(shù)
對(duì)于標(biāo)量函數(shù)而言,有一堆大括號(hào)括起來的 A 進(jìn)行了某種操作,這個(gè)操作是加上了一個(gè)由倒三角符號(hào)和約等于符號(hào)連接起來的東西,基于這樣的情況,由倒三角符號(hào)、點(diǎn)運(yùn)算符以及包裹著一堆大括號(hào)的 A 所構(gòu)成的表達(dá)式的取值能夠被控制 。
場(chǎng)源導(dǎo)致的勢(shì)
(假 定 無 窮 遠(yuǎn) 處 勢(shì) 為 零),(({{r}}))等于,((frac{1}{4pi}))乘以,對(duì),((frac{rho({{r}} ')}{ leftlvert {{r}} - {{r}}'rightrvert }))進(jìn)行,((intj5hblzv{V}'))的積分 。
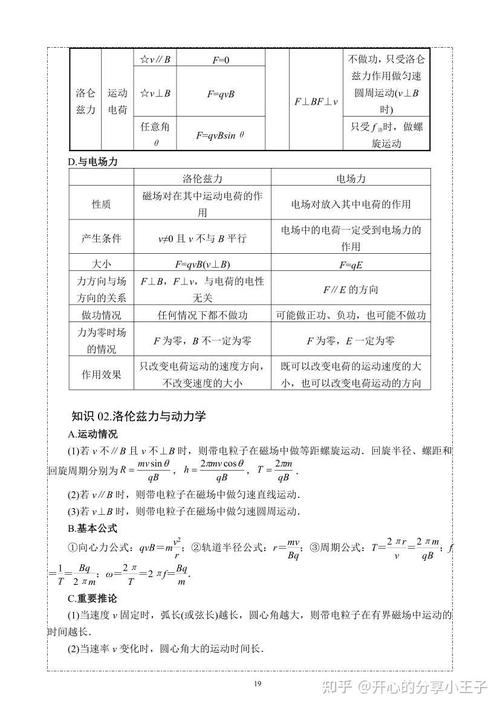
大括號(hào)括起來的A,對(duì)于大括號(hào)括起來的r的函數(shù)值,等于4π分之μ?,對(duì)函數(shù)值是以下情況的積分:被積函數(shù)是大括號(hào)括起來的j對(duì)于大括號(hào)括起來的r撇的函數(shù)值,除以大括號(hào)括起來的r減去大括號(hào)括起來的r撇的絕對(duì)值,積分微元是dV撇 。(假定取規(guī)范 梯度算符點(diǎn)乘大括號(hào)括起來的A等于 ?) 。
勢(shì)的方程
(假定無窮遠(yuǎn)處勢(shì)為零)梯度的平方的負(fù)一倍等于負(fù)的密度除以某個(gè)東西 , 。
負(fù)的真空磁導(dǎo)率乘以電流密度矢等于,取規(guī)范為矢量算符點(diǎn)乘矢勢(shì)矢等于零的情況下,矢量算符的平方作用于矢勢(shì)矢 。
勢(shì)的定義
引入勢(shì)的數(shù)學(xué)考量是(詳見 與 “矢量分析總結(jié) ”):
靜電場(chǎng)天然滿足這些條件,磁場(chǎng)天然也滿足這些條件,所以靜電場(chǎng)能夠分別定義電勢(shì),磁場(chǎng)能夠分別定義磁勢(shì)。
物理上的考量參考 “電勢(shì)、電勢(shì)能 ”。
于電場(chǎng)與電勢(shì)的關(guān)系而言,極易看出,靜電場(chǎng)實(shí)際上唯有一個(gè)自由度,并非如看上去那般是三個(gè),分別為 E_x、E_y、E_z 。
勢(shì)的任意性
因?yàn)殡姾芍苯痈惺艿降氖菆?chǎng)并非勢(shì)(見下面的“洛倫茲力”),所以只要能夠獲取相同的場(chǎng),勢(shì)的取值具備一定的靈活性。比如說,鑒于({{E}} = - \nabla $),即便勢(shì)加上一個(gè)常數(shù),依舊存在({{E}} = - \nabla (+) = - \nabla - \nabla = - \nabla $),也就是相應(yīng)的電場(chǎng)不會(huì)發(fā)生改變。這樣一來,電勢(shì)能夠始終相差一個(gè)常數(shù),卻不會(huì)對(duì) “實(shí)質(zhì)性結(jié)果” 造成改變。這跟我們進(jìn)行不定積分操作時(shí),常常會(huì)得出一個(gè)積分常數(shù) $C$ 的情況十分相像。又好比針對(duì)函數(shù)求導(dǎo)之際,常數(shù)項(xiàng)不會(huì)對(duì)導(dǎo)函數(shù)產(chǎn)生影響。將選取常數(shù)的方式稱作 “規(guī)范”,依據(jù)具體的場(chǎng)合情形,我們會(huì)挑選適宜恰當(dāng)?shù)囊?guī)范,以此用來簡(jiǎn)化計(jì)算過程。在靜場(chǎng)環(huán)境當(dāng)中,我們通常會(huì)設(shè)定電勢(shì)在無窮遠(yuǎn)的地方為零,并且要使磁勢(shì)滿足 $ {nabla}{cdot} {{A}} = 0$ 。
勢(shì)的方程
把勢(shì)的定義代入方程組,再借助數(shù)學(xué)方面的一些技巧,如此一來,便能夠得到與之對(duì)應(yīng)的勢(shì)的方程。比如說對(duì)于電勢(shì):有這樣一組式子$$left {begin{}{{E}} &= - \nabla \\{nabla}{cdot} {{E}} &= frac{rho}{}\end{}right.\{nabla}^2 = -frac{rho}{}是成立的~。$$請(qǐng)注意,這里方程中的一些符號(hào)表述可能不太規(guī)范明了,應(yīng)結(jié)合具體的物理知識(shí)背景來準(zhǔn)確理解其確切含義~。電勢(shì)的相關(guān)方程在電學(xué)等領(lǐng)域有著極為重要的作用,是進(jìn)一步深入研究電場(chǎng)等電現(xiàn)象的關(guān)鍵基礎(chǔ)~。
磁勢(shì)的情況也是同樣的道理,然而卻需要運(yùn)用更為巧妙的數(shù)學(xué)技巧以及規(guī)范,具體的證明過程依照慣例是留給讀者的:有這樣一組式子,其中(left{begin{array}{}{{B}} = {nabla}{times} {{A}} \{nabla}{times} {{B}} = mu_0 {{j}} \{nabla}{cdot} {{A}} = 0end{array}right.),通過推導(dǎo)得出({nabla}^2 {{A}} = -mu_0 {{j}}) 。因?yàn)榇艅?shì)( {{A}})是一個(gè)矢量,故而磁勢(shì)的方程實(shí)際上涵蓋三個(gè)標(biāo)量方程(在直角坐標(biāo)系下):(nabla^2 {{A}} = - mu_0 {{j}}) ,具體為(left{begin{array}{}= {nabla}^2 A_x = -mu_0 j_x\= {nabla}^2 A_y = -mu_0 j_y\= {nabla}^2 A_z = -mu_0 j_zend{array}right.~ 。) 。
場(chǎng)源導(dǎo)致的勢(shì)
從原則上來說,“場(chǎng)源致使的勢(shì)”屬于對(duì)應(yīng)勢(shì)的方程所能產(chǎn)生的解高中物理電磁場(chǎng)設(shè)計(jì),然而要是這么去做的話,速度就會(huì)變得遲緩起來。憑借電場(chǎng)的性質(zhì),借助勢(shì)的定義,依據(jù)電勢(shì)與積分路徑無關(guān)的特性便能輕易得出“電荷導(dǎo)致的勢(shì)”,這同樣是我們于高中以及大物中所知曉的辦法:等于對(duì)矢量(E)與矢量(dl)做點(diǎn)積的積分,等于(frac{1}{4pi})乘以從電勢(shì)源取出測(cè)試電荷的距離(R)分之電荷量(q),并將之推廣為連續(xù)形式,等于(frac{1}{4pi})乘以對(duì)電荷密度(rho)與從場(chǎng)點(diǎn)到場(chǎng)源點(diǎn)距離(R)分之一的乘積進(jìn)行體積分,根據(jù)磁勢(shì)方程與電勢(shì)的類似性,通過類比就能得到“電流導(dǎo)致的磁勢(shì)”。如此操作避免了求解偏微分方程的困難。
圖 2:源->勢(shì)->場(chǎng)
4. 洛倫茲力
一個(gè)處于電磁場(chǎng)里的點(diǎn)電荷、其受力情況是由洛倫茲力公式予以給出的,該公式為{{F}} = q ( {{E}} + {{v}} \times {{B}} )~,要留意此公式里并不涵蓋點(diǎn)電荷處于靜止?fàn)顟B(tài)或者勻速運(yùn)動(dòng)狀態(tài)之時(shí)自身所產(chǎn)生的電磁場(chǎng),而且當(dāng)點(diǎn)電荷進(jìn)行非勻速運(yùn)動(dòng)之際會(huì)產(chǎn)生輻射也就是電磁波,并且這個(gè)輻射又將反過來作用于點(diǎn)電荷之上。以能量守恒的角度去講,電荷因產(chǎn)生輻射致使能量有所損失,進(jìn)而言之動(dòng)能肯定會(huì)降低,故而其輻射針對(duì)自身的力總體而言必定是一種阻力。但在通常情形下,我們?cè)O(shè)定這個(gè)輻射的功率足夠地小,從而讓該效應(yīng)能夠被忽略不計(jì) ,。
對(duì)于電荷呈連續(xù)分布的情況,我們?nèi)ッ枋鰡挝惑w積(也就是“一小塊”)里電荷所受到的洛倫茲力,這等價(jià)于將上式兩邊進(jìn)行“同除以” ( ,lrrpznl{V} ) 的操作,。先看這個(gè),{{f}}等于,xr77njp除以{{F}},再除以lnh57jn與V的運(yùn)算結(jié)果,它又等于,b5lnpl7除以q,除以vxzj7hd與V的運(yùn)算,乘以{{E}}加上{{v}}與{{B}}的叉乘,等于ρ乘以{{E}}加上{{v}}與{{B}}的叉乘,等于ρ{{E}}加上{{j}}與{{B}}的叉乘 , 。
有時(shí)候,我們做出這樣的假定,那就是電流是伴隨著異號(hào)的靜止電荷的,所以呢,電流從總體上來說是不帶靜電荷的,并且也不會(huì)產(chǎn)生電場(chǎng)。
防杠聲明:嚴(yán)格來說,在相對(duì)論中是質(zhì)量-能量守恒。
和靜電場(chǎng)里能夠隨意放置電荷不一樣,在靜磁場(chǎng)當(dāng)中,我們沒辦法“隨意放置”電流,而是一定要讓電流形成環(huán)狀,或者延伸至無窮遠(yuǎn)的地方。要是設(shè)計(jì)的“電路”沒有形成環(huán),那么依據(jù)電荷守恒,區(qū)域內(nèi)的電荷密度肯定會(huì)發(fā)生變化,進(jìn)而不再屬于靜場(chǎng)問題。這同樣是為何這個(gè)公式實(shí)際上無法精確描述“單個(gè)運(yùn)動(dòng)電荷的磁場(chǎng)”的緣由 。
為啥那個(gè)表示旋度的符號(hào)與電場(chǎng)強(qiáng)度矢量叉乘結(jié)果為零的方程沒了呢,是由于在引入電勢(shì)概念之際高中物理電磁場(chǎng)設(shè)計(jì),我們已然運(yùn)用了此方程,即對(duì)于任意標(biāo)量函數(shù)而言,其梯度的旋度一直都為零制度大全,也就是那個(gè)表示旋度的符號(hào)與梯度叉乘等于零 。
David , to , 4ed
給讀者朋友們講,小時(shí)百科始終都保持著所有的內(nèi)容是免費(fèi)且沒有廣告的狀態(tài),這種情況致使我們處于一種嚴(yán)重虧損的情形之中。要是一直這樣持續(xù)下去的話,極有可能終究使得我們不得不去選擇大量投放廣告以及實(shí)行內(nèi)容付費(fèi)等等之類的做法。所以呢,我們懇請(qǐng)廣大的讀者朋友們能夠熱心地進(jìn)行打賞,從而讓網(wǎng)站能夠朝著健康的方向發(fā)展下去。要是每一位看到這條信息的讀者都能夠大方地拿出20元來進(jìn)行打賞,那么我們一個(gè)星期就能夠擺脫虧損的局面,并且在接下來的一整年時(shí)間里可以繼續(xù)向所有讀者免費(fèi)提供高質(zhì)量的內(nèi)容 。只是令人可惜的是,僅有不到百分之1的讀者樂意捐款,這群讀者的付出,讓百分之99的讀者能夠不付費(fèi)就獲取知識(shí),我們于此致以謝意。
