

摘要你好,小鄭就為你們解答關(guān)于化學(xué)動(dòng)能定律及應(yīng)用,化學(xué)動(dòng)能定律公式相信好多男子伴還不曉得,如今讓我們一上去瞧瞧吧!1、動(dòng)能具有瞬時(shí)性,是
你好,小鄭就為你們解答關(guān)于化學(xué)動(dòng)能定律及應(yīng)用,化學(xué)動(dòng)能定律公式相信好多男子伴還不曉得,如今讓我們一上去瞧瞧吧!
1、動(dòng)能具有瞬時(shí)性,是指力在一個(gè)過(guò)程中對(duì)物體所做的功等于在這個(gè)過(guò)程中動(dòng)能的變化。
2、動(dòng)能是狀態(tài)量,無(wú)負(fù)值。
3、合外力(物體所受的外力的總和,依照方向以及受力大小通過(guò)正交法[1]能估算出物體最終的合力方向及大小)對(duì)物體所做的功等于物體動(dòng)能的變化。
4、即末動(dòng)能減初動(dòng)能。
5、表達(dá)式其中,Ek2表示物體的末動(dòng)能,Ek1表示物體的初動(dòng)能。
6、△W是動(dòng)能的變化,又稱(chēng)動(dòng)能的增量,也表示合外力對(duì)物體做的總功。
7、1.動(dòng)能定律研究的對(duì)象是單一的物體,或則是可以堪比單一物體的物體系。
8、2.動(dòng)能定律的估算式是方程,通常以地面為參考系。
9、3.動(dòng)能定律適用于物體的直線(xiàn)運(yùn)動(dòng),也適應(yīng)于曲線(xiàn)運(yùn)動(dòng);適用于恒力做功,也適用于變力做功;力可以是分段作用,也可以是同時(shí)作用,只要可以求出各個(gè)力的正負(fù)代數(shù)和即可,這就是動(dòng)能定律的優(yōu)越性。
10、一些疑惑點(diǎn)說(shuō)明1.動(dòng)能是標(biāo)量,本身不可以用來(lái)進(jìn)行矢量分解,但動(dòng)能定律的運(yùn)用中,可先求各分力在各自運(yùn)動(dòng)方向上所做的功,再來(lái)求代數(shù)和。
11、2.動(dòng)能定律一定是合外力做功,對(duì)于在豎直面內(nèi)有繩牽引的圓周運(yùn)動(dòng)而言,之所以可以只用重力做功來(lái)列式是由于,直接求合力做功時(shí),合力方向,大小都在改變,難以直接求解,用分力求解時(shí)拉力垂直于運(yùn)動(dòng)方向,該分力做功為0,只剩重力做功。
12、而合力不可能沿切線(xiàn)方向,當(dāng)合力沿切線(xiàn)方向時(shí),畫(huà)圖可知,此時(shí)沒(méi)有力提供向心力。
13、雖然弧形寬度小于豎直方向上的位移,但采用合力求功并不會(huì)大于重力做功的數(shù)值。
14、3.動(dòng)能定律要考慮內(nèi)力做功.諸如A物體放置在B物體上,合外力對(duì)B施加aN,兩物體間有磨擦力bN,B物體運(yùn)動(dòng)了c米,發(fā)生相對(duì)滑動(dòng)為d米,A對(duì)B做的負(fù)功小于B對(duì)A做的正功,所以系統(tǒng)總能量消耗了。
15、2定律1編輯內(nèi)容質(zhì)點(diǎn)系所有外力做功之和加上所有內(nèi)力做功之和等于質(zhì)點(diǎn)系總動(dòng)能的改變量。
16、和質(zhì)點(diǎn)動(dòng)能定律一樣,質(zhì)點(diǎn)系動(dòng)能定律只適用于慣性系,由于外力對(duì)質(zhì)點(diǎn)系做功與參照系選擇有關(guān),而內(nèi)力做功卻與選擇的參照系無(wú)關(guān),由于力總是成對(duì)出現(xiàn)的,一對(duì)斥力和反斥力(內(nèi)力)所做功代數(shù)和取決于相對(duì)位移,而相對(duì)位移與選擇的參照系無(wú)關(guān)。
17、動(dòng)能定律的內(nèi)容:所有外力對(duì)物體總功,(也稱(chēng)作合外力的功)等于物體的動(dòng)能的變化。
18、動(dòng)能定律的物理表達(dá)式:動(dòng)能定律只適用于宏觀低速的情況,由于在相對(duì)論中F=ma是不創(chuàng)立的[1],質(zhì)量隨速率改變。
19、而動(dòng)量定律可適用于世界上任何情況。
20、(前提是系統(tǒng)中外力之和為0)物體因?yàn)檫\(yùn)動(dòng)而具有的能量.用Ek表示。
21、表達(dá)式:,動(dòng)能是標(biāo)量也是狀態(tài)量。
22、單位:焦耳(J)1kg*m^2/s^2=1J(2)動(dòng)能定律內(nèi)容:合外力做的功等于物體動(dòng)能的變化。
23、表達(dá)式:適用范圍恒力做功、變力做功、分段做功、全程做功等均可適用。
24、動(dòng)量定律與動(dòng)能定律的區(qū)別動(dòng)量定律Ft=mv2-mv1反映了力對(duì)時(shí)間的累積效應(yīng),是力在時(shí)間上的積分。
25、動(dòng)能定律Fs=1/2mv^2-1/2mv0^2反映了力對(duì)空間的累積效應(yīng),是力在空間上的積分。
26、3質(zhì)點(diǎn)編輯內(nèi)容:合外力做功等于物體動(dòng)能的增量.表達(dá)式:△W=△Ep1.定律的使用對(duì)象是質(zhì)點(diǎn).2.合外力的求法符合平行四邊形法則.2‘.∑W=W1+W2+W3+...+Wn3.功是力在空間上的積累療效,亦稱(chēng)為力對(duì)位移的積分,這從功的定義式(如W=Fscosa)中可以看出,因而動(dòng)能定律描述的是一段過(guò)程的變化。
27、4.動(dòng)能沒(méi)有負(fù)值,但動(dòng)能增量(末動(dòng)能減初動(dòng)能)可能為正,可能為負(fù),也可能是零。
28、4‘.△Ek表示動(dòng)能的增量。
29、一般△都表示末狀態(tài)量除以初狀態(tài)量.5.動(dòng)能的增量為零,則合外力做功為零。
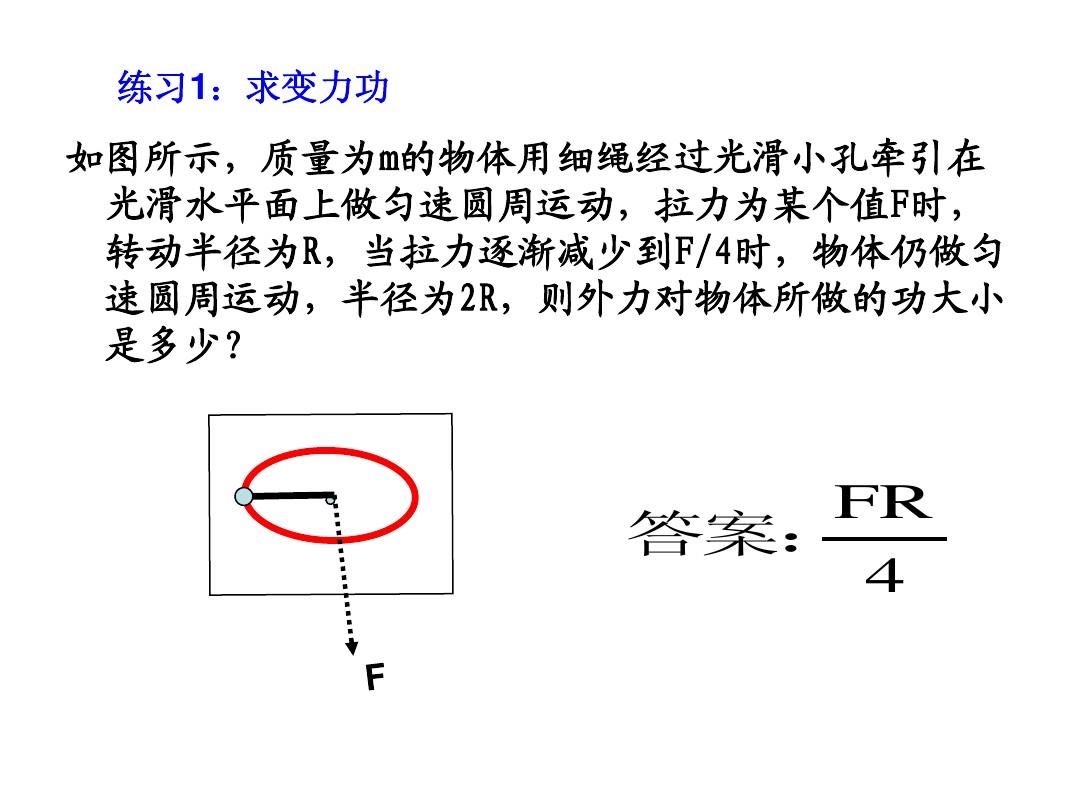
30、但此時(shí)合外力不一定為零,各分力做功也不一定都為零動(dòng)能定理的應(yīng)用,請(qǐng)非常注意.(舉例:水平面上的勻速圓周運(yùn)動(dòng))6.應(yīng)用動(dòng)能定律時(shí),要注意參考系的一致。
31、即所有數(shù)學(xué)量(如位移,速率)都取自同一參考系(參照物)。
32、7.參考系應(yīng)選用慣性系。
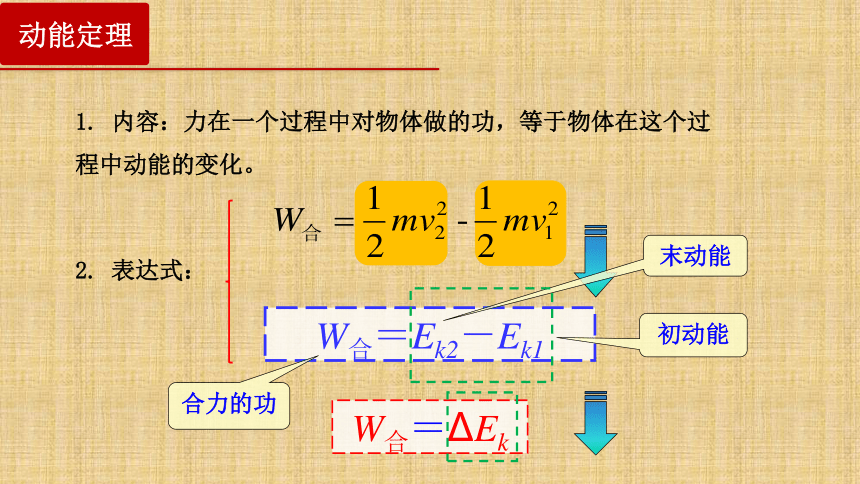
33、8.動(dòng)能定律描畫(huà)了合外力的功與動(dòng)能之間的變化關(guān)系。
34、同樣的,其他性質(zhì)的力和其相應(yīng)能量之間的也有類(lèi)似的恒等關(guān)系式,我們也稱(chēng)其為功能關(guān)系。
35、在動(dòng)能定律的基礎(chǔ)上運(yùn)用功能關(guān)系進(jìn)行恒等變換,加以條件限制,便得出了一系列守恒定理,如機(jī)械能守恒定理等。
36、條件限制對(duì)于這種守恒定理是很重要的,如機(jī)械能守恒定理的條件是除重力、彈力外沒(méi)有其他力做功。
37、9.動(dòng)能定律、功能關(guān)系、能量守恒定理,盡管其表現(xiàn)方式和意義都不盡相同,但都是等價(jià)的。
38、解決問(wèn)題時(shí),只需采用其中一個(gè)即可。
39、4系統(tǒng)編輯由質(zhì)點(diǎn)的動(dòng)能定律,我們還可以得出更通常的系統(tǒng)的動(dòng)能定律。
40、系統(tǒng)各組分合外力做功的代數(shù)和等于系統(tǒng)各組分動(dòng)能增量的代數(shù)和∑(∑W)=∑(△Ek)在大多數(shù)情況下,系統(tǒng)各組分之間互相做的功其代數(shù)和都是零,此時(shí)應(yīng)用系統(tǒng)的動(dòng)能定律更為便捷.但當(dāng)系統(tǒng)各組分之間互相做功代數(shù)和不為零(如存在彈簧,互相引力、斥力等)的情況,應(yīng)考慮內(nèi)力做功動(dòng)能定理的應(yīng)用,非常注意!FScosα代表作用在運(yùn)動(dòng)質(zhì)點(diǎn)上的合外力的功(α代表力和水平方向的傾角)。
41、應(yīng)從動(dòng)能定律深入領(lǐng)會(huì)“功”和“動(dòng)能”兩個(gè)概念之間的區(qū)別和聯(lián)系。
42、動(dòng)能是反映物體本身運(yùn)動(dòng)狀態(tài)的數(shù)學(xué)量。
43、此定律彰顯了功和動(dòng)能之間的聯(lián)系。
44、稱(chēng)為定律的緣由是由于它是從牛頓定理,經(jīng)物理嚴(yán)格推論下來(lái)的,并不能擴(kuò)大其應(yīng)用范圍。
45、由于動(dòng)能定律不涉及物體運(yùn)動(dòng)過(guò)程中的加速度和時(shí)間,不論物體運(yùn)動(dòng)的路徑怎樣,因此在只涉及位置變化與速率的熱學(xué)問(wèn)題中,應(yīng)用動(dòng)能定律比直接運(yùn)用牛頓第二定理要簡(jiǎn)單。
46、5解題步驟編輯剖析(1)確定研究對(duì)象,研究對(duì)象可以是一個(gè)質(zhì)點(diǎn)(單體)也可以是一個(gè)系統(tǒng)。
47、(2)剖析研究對(duì)象的受力情況和運(yùn)動(dòng)情況,是否是求解“力、位移與速率關(guān)系”的問(wèn)題。
48、(3)若是,按照∑W=△Ek1列式求解。
49、推導(dǎo)對(duì)于勻加速直線(xiàn)運(yùn)動(dòng)有:由牛頓第二運(yùn)動(dòng)定理得F=ma①勻加速直線(xiàn)運(yùn)動(dòng)規(guī)律有:s=((v2)^2-(v1)^2)/(2a)②①×②得:Fs=(1/2)m(v2)^2-(1/2)m(v1)^2外力做功W=Fs,記Ek1=(1/2)m(v1)^2,Ek2=(1/2)m(v2)^2即W=Ek2-Ek1=△Ek對(duì)于非勻加速直線(xiàn)運(yùn)動(dòng):進(jìn)行無(wú)限細(xì)分成n段,于是每段都可看成是勻加速直線(xiàn)運(yùn)動(dòng)(微分思想)對(duì)于每段運(yùn)動(dòng)有:W1=Ek1-Ek0W2=Ek2-Ek1……Wn=Ekn-Ekn-1將上式全部相乘得∑W=Ekn-Ek0=△Ek推論完畢。
本文就提到這兒,希望你們會(huì)喜歡。