貢獻者：addis;零穹
預備知識質(zhì)心，角動量定律，勻加速直線運動
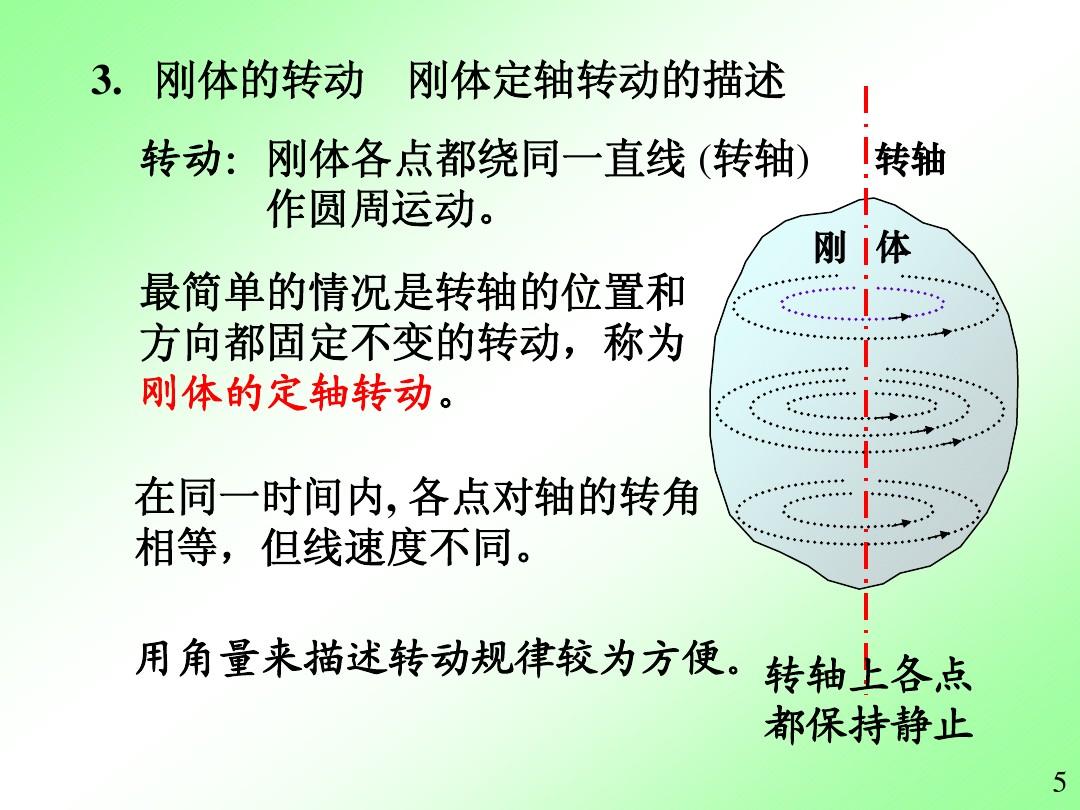
1.質(zhì)心的定軸轉動
若質(zhì)心繞固定軸轉動，這么質(zhì)心的位置只需一個變量即可完全確定（一個自由度），我們令該變量為拐角$theta$。$theta$關于時間$t$的行列式就是質(zhì)心定軸旋轉的角速率$omega$。我們還可以定義角速率$omega$關于時間的行列式（即$theta$關于時間的二階行列式）為角加速度（），記為$alpha$
begin{}alpha=frac{txrzbvzd^{2}{theta}}{txrzbvzd{t}^{2}}~.end{}
我們可以把質(zhì)心的定軸轉動類比質(zhì)點的直線運動，把$theta$，$omega$和$alpha$分別類比為直線運動中的位置$x$，速率$v$和加速度$a$，由于后三個變量之間的物理關系是完全相同的：$v,omega$分別是$x,theta$的一階求導，而$a,alpha$分別是$x,theta$的二階行列式。
于是我們可以立刻類比勻加速直線運動得到勻變速定軸轉動（即$alpha$為常數(shù)）的一些公式，如
begin{}omega=+alphat~,\theta=+t+\alphat^2~,\^2-^2=2alpha(-)~.end{}
在以上三個標量的基礎上，我們可以定義它們的矢量方式${{theta}}$，${{omega}}$和${{alpha}}$，令它們的方向為轉軸的方向，用左手定則來判別。在質(zhì)心定軸轉動的約束下，三個矢量的方向都是轉軸的方向，所以通常用標量就足夠了，這就好比討論質(zhì)點的直線運動時，用標量表示位置物理旋轉運動公式，速率，加速度就夠了。只有當轉軸會隨時間改變時才有必要使用矢量方式（見“慣性張量”）。
要判定質(zhì)心上任意一點的速率，使用即可（見）
begin{}{{v}}={{omega}}\times{{r}}={{omega}}\times{{r}}_bot~.end{}
圖1：質(zhì)心定軸旋轉時任意一點的線速率
以上只是運動學而不含動力學，也就是并沒有考慮力和運動之間的關系。下邊我們將通過角動量定律得出類似牛頓第二定理的動力學公式：
begin{}tau_z=Ialpha~,end{}
其中$tau_z$是外力對系統(tǒng)的合扭力在轉軸方向（令為$z$軸）的份量，對應牛頓第二定理中的力$F$；$I$（有時也用$J$）是一個和質(zhì)心的質(zhì)量分布有關的量叫轉動力矩，對應牛頓第二定理熱學中的質(zhì)量$m$。2.角動量的軸向份量與轉動力矩
要討論質(zhì)心的定軸轉動和所受轉矩之間的關系，我們須要先來看角動量矢量在轉軸正方向的份量。之后會曉得若定軸旋轉的質(zhì)心的質(zhì)量分布關于轉軸有某種旋轉對稱，這么質(zhì)心的角動量矢量必將是平行于轉軸的，但是對于更通常的質(zhì)心（如），定軸轉動時的角動量矢量就未必與轉軸平行（如）。所以為了簡單起見我們先討論其軸向的份量，完整的矢量關系之后會在“慣性張量”中見到。
我們把轉軸的某個正方向定義為$z$軸正方向，單位矢量記為$hat{{{z}}}$。對于質(zhì)心上的單個質(zhì)點，角動量在$z$方向的份量為
begin{}L'_{z}={{L}}\cdothat{{{z}}}=({{r}}\times{{p}})\cdothat{{{z}}}~.end{}
首先把質(zhì)點的位矢在$z$方向和垂直$z$方向分解（稱為水平方向），${{r}}={{r}}_z+{{r}}_bot$。因為${{p}}$仍然沿水平方向，按照叉乘的幾何定義，${{r}}_z\times{{p}}$也是沿水平方向，只有${{r}}_bot\times{{p}}$沿$z$方向。另外，在圓周運動中，直徑仍然與速率垂直，所以${{r}}_bot$一直與${{p}}$垂直。得出推論
begin{}L'_z=leftlvert{{r}}_botrightrvertleftlvert{{p}}rightrvert=mr_botv=mr_bot^2omega~.end{}
現(xiàn)今討論質(zhì)心的角動量，若把質(zhì)心分成無數(shù)小塊，每小塊的質(zhì)量分別為$m_i$，離軸的距離$r_{boti}=sqrt{x_i^2+y_i^2}$，角動量軸向份量為$L_{iz}$則質(zhì)心的弱冠動量$z$份量為
begin{}L_z=sum_iL_{iz}=omegasum_im_ir_{boti}^2~,end{}
用定積分寫成
begin{}L_z=omegaintr_bot^2,txrzbvzd{m}=omegaintr_bot^2rho({{r}}),txrzbvzd{V}~.end{}
定義質(zhì)心繞固定軸旋轉的轉動力矩（of）為
begin{}I=intr_bot^2,txrzbvzd{m}=intr_bot^2rho({{r}}),txrzbvzd{V}~.end{}
注意角動量的大小除了取決于質(zhì)心的質(zhì)量分布，還取決于轉軸的位置和方向。最后得質(zhì)心沿軸方向的角動量份量為
begin{}L_z=Iomega~,end{}
可見$L_z$和旋轉角速率成反比。3.角加速度與扭矩
預備知識單擺
要剖析質(zhì)心的轉動與質(zhì)心所受外力的關系，就要對系統(tǒng)使用角動量定律。在這兒“系統(tǒng)”指的就是質(zhì)心本身，不包含任何相對質(zhì)心運動的物體。我們要分辨兩種轉軸：幾何轉軸是一條假想的有正方向的幾何直線，質(zhì)心上任意一點都繞該直線做圓周運動，任何做定軸轉動的質(zhì)心都存在幾何轉軸。化學轉軸可以有粗細有質(zhì)量、也可以對質(zhì)心提供約束力。化學轉軸不是質(zhì)心做定軸轉動所必須的，比如真空無重力環(huán)境中自由旋轉的物體有幾何轉軸但不須要任何化學轉軸。
約束物體做定軸轉動的機械結構可能是多種多樣的，比如通過軸承將物體套在一根固定的桿上，此時桿則不屬于質(zhì)心的一部份，桿對旋轉體的所有斥力都視為系統(tǒng)外力。另一種太原小異的情況諸如桿固定在旋轉體上一起轉動，而桿兩端套在固定的軸承上，此時桿可以視為質(zhì)心的一部份，故無需剖析桿和物體之間的互相作用，軸承對桿的任何斥力都視為系統(tǒng)外力。又譬如一個環(huán)型物體通過滑輪固定在一個環(huán)型軌道上轉動，此時滾輪對物體的力為外力，幾何轉軸處沒有任何其他結構。其實無論機械結構有多么復雜，我們只須要把機械結構中不發(fā)生形變的、作為整體繞幾何軸旋轉的部份看成質(zhì)心，外部對它的一切力（矩）都視為系統(tǒng)外力（矩），這么以下的剖析就是組建的。
對系統(tǒng)使用“角動量定律”的，注意等號兩側是矢量，所以各個份量必須相等，我們有
begin{}tau_z=frac{txrzbvzd{L_z}}{txrzbvzd{t}}~,end{}
將代入，并借助角加速度的定義得
begin{}tau_z=Ialpha~.end{}
這就是質(zhì)心定軸轉動的動力學多項式，其方式可類比質(zhì)點做直線運動時的牛頓第二定理$F=ma$：$tau_z$可以類比力$F$，$I$類比質(zhì)量$m$，$alpha$類比加速度$a$。角動量軸向份量守恒
在定軸轉動的情況下，依據(jù)，當系統(tǒng)外對系統(tǒng)扭矩的軸向份量$tau_z$為零時，角動量的軸向份量$L_z$守恒。這意味著質(zhì)心的角加速度為零（），也就是質(zhì)心做勻速轉動或靜止。類比到質(zhì)點的直線運動就是當$F=ma$中外力$F=0$時，加速度為零，質(zhì)點做勻速運動，動量守恒。
可見和“勻速運動不須要外力維持”一樣，勻速轉動也并不須要轉軸方向的外扭力維持。但是在日常生活中，正如水平直線軌道上具有初速率的滑塊會因為與軌道的磨擦力，空氣阻力等各類外力最終停止運動，具有初始角速率的物體也會在機械磨擦、空氣阻力等外扭矩的作用下最終停止轉動，這與上述動量守恒并不矛盾。
例1化學擺
化學擺（），也叫復擺（）。如，已知質(zhì)量為$M$的質(zhì)心關于某轉軸的轉動力矩為$I$，轉軸到質(zhì)心剛體的寬度為$r_c$，轉軸和形心的連線與豎直方向傾角為$theta$，求質(zhì)心的運動多項式。
圖2：化學擺
首先我們把質(zhì)心看做質(zhì)點系，作剛體到轉軸的垂線，以垂足為座標原點，以轉軸指向紙內(nèi)的方向為$z$軸正方向，令剛體的位置矢量為${{r}}_c$（與轉軸垂直），估算重力對質(zhì)心的合扭矩為（）
begin{}{{tau}}=M{{r}}_c\times{{g}}~.end{}
因為${{r}}_c$與轉軸垂直，${{tau}}$與轉軸平行，所以
begin{}tau_z=Mgr_csintheta~.end{}
這說明，質(zhì)心所受轉矩相當于質(zhì)量為$M$，厚度為$r_c$的單擺所受的扭力。代入得質(zhì)心擺的運動多項式為
begin{}Iddottheta=Mgr_csintheta~,end{}
可以驗證當質(zhì)心的質(zhì)量全部集中在剛體時（$I=Mr_c^2$）我們就得到了單擺的運動多項式。
若已知初始角度和角速率，由質(zhì)心定軸轉動的動能定律可以求得任何角度時的角速率，詳見。
例2袋子傾倒
如，一長方體袋子初始時夾角為$$，以初速率0無滑動傾倒，求其運動多項式。
圖3：袋子傾倒
這和屬于同一模型，公式不再贅言。事實上，長方體袋子的旋轉運動和其截面長圓形的旋轉一致，這本質(zhì)上是一個二維問題。初始時若袋子的剛體在轉軸一側時，袋子必然順秒針傾倒，反之逆秒針傾倒。若初始時剛體正好在轉軸上方，這么這是一個不穩(wěn)定平衡，任何微小的擾動就會使袋子向某兩側傾倒。
例3
未完成：未完成。鏈接到這兒。
圖4：請?zhí)砑訄D片描述
4.垂直軸的角動量
以上的討論中，我們有意避開討論垂直軸方向的角動量份量$L_x,L_y$。通常情況下，我們不能保證她們是守恒的。在一些特殊情況下，比如質(zhì)心的形狀和質(zhì)量分布關于轉軸呈某種軸對稱物理旋轉運動公式，這么容易證明質(zhì)心（關于任意固定點）的弱冠動量${{L}}$只可能延轉軸方向，即$L_x=L_y=0$守恒。
在一些不對稱的情況下，比如一個傾斜的細桿繞轉軸旋轉，轉軸就須要對細桿施加一個不停旋轉的扭矩，細桿也會對軸施加一個反扭矩，這類似于斥力和反斥力，詳見“剛體定軸轉動2”。
比如圓盤、長圓形、正三角形等繞對稱軸旋轉
致讀者：小時百科始終以來堅持所有內(nèi)容免費，這造成我們處于嚴重的巨虧狀態(tài)。長此往年很可能會最終造成我們不得不選擇大量廣告以及內(nèi)容付費等。為此，我們懇求廣大讀者熱心打賞，使網(wǎng)站得以健康發(fā)展。假如見到這條信息的每個讀者能慷慨打賞10元，我們一個禮拜內(nèi)才能脫離巨虧，并保證在接出來的一整年里向所有讀者繼續(xù)免費提供優(yōu)質(zhì)內(nèi)容。但遺憾的是只有不到1%的讀者樂意籌款，她們的付出幫助了99%的讀者免費獲取知識，我們在此表示謝謝。