斯涅爾定理告訴我們折射率與給定介質對的入射角、折射角和折射率之間的關系。 我們知道,當光從一種介質傳播到另一種介質時,它會發生折射或彎曲。 斯涅爾定理預測了曲率的程度。 它也稱為折射定理。 1621年,維勒伯德·斯內爾發現了折射定理,稱為斯內爾定理。
斯涅爾定理被定義為“對于給定的顏色和給定的介質對,入射角的余弦與折射角的余弦之比是一個常數”。 斯涅爾定理的公式表示為:
其中 i 是入射角,r 是折射角。 該常數稱為第二介質相對于第一介質的折射率。
下面是示意圖:
斯涅爾定理公式是從費馬原理推導出來的。 費馬原理強調“光以最短的路徑傳播,花費最少的時間”。
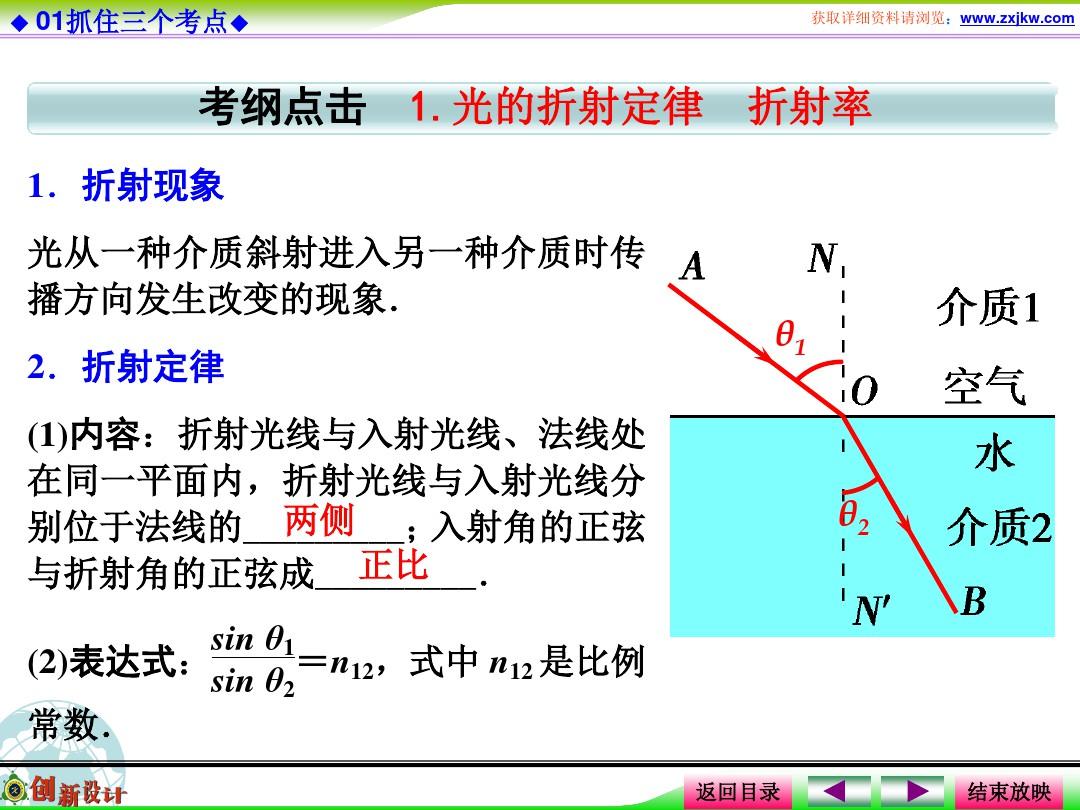
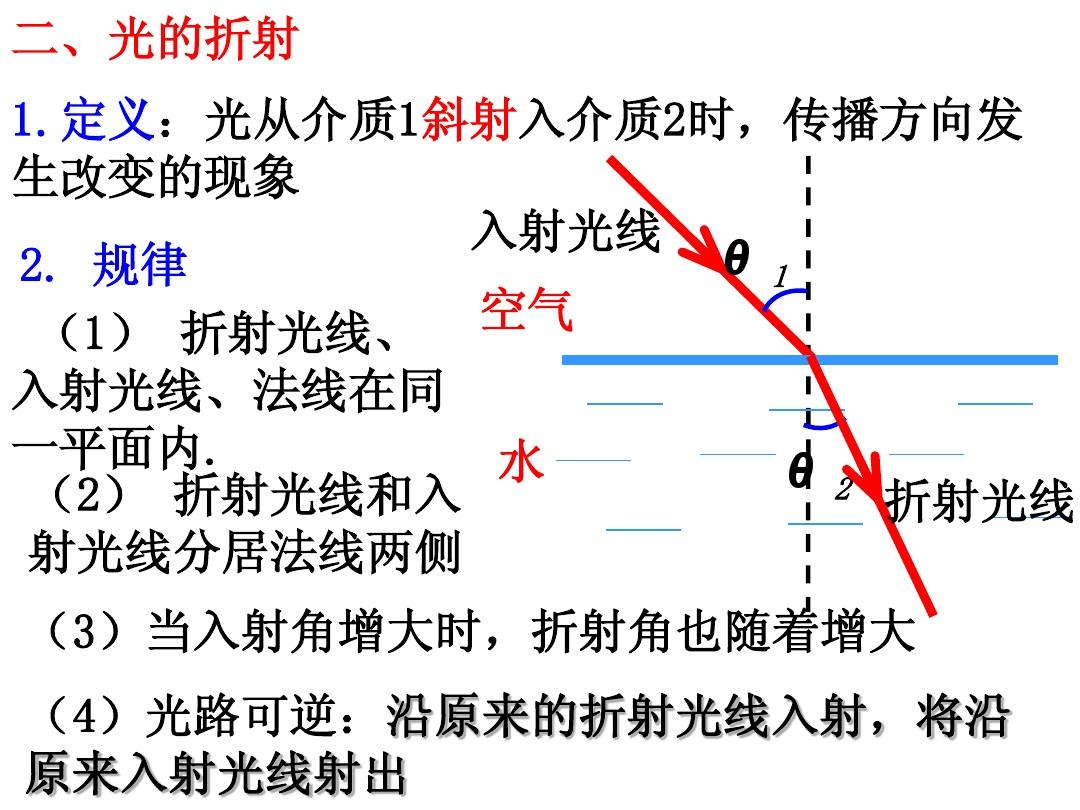
表面上的法線用于檢測折射光線在接觸點處形成的角度。 n1和n2是兩種不同的介質,會影響折射。 θ1為入射角; θ2是折射角。
斯涅爾定理公式在現實生活中的應用:
斯涅爾定理在數學中有著廣泛的應用,特別是在光學領域。 用于太陽鏡、隱形太陽鏡、相機、彩虹等光學器件。 有一種稱為折射計的儀器光折射的例子和原理,它使用斯涅爾定律來估計液體的折射率。 它仍然在后期制作行業中使用。
已解決的示例:
問題 1:如果光線以 14° 的角度折射且折射率為 1.2光折射的例子和原理,則估計入射角。
解決方案:考慮,
折射角r=14°
折射率μ=1.2
使用斯涅爾定理公式,
問題2:若入射角為25°,折射角為32°,求介質的折射率。
解決方案:考慮,
入射角,i=25°
折射角,r=32°
使用斯涅爾定理公式,
