1982年，肯尼思·威爾遜因其偉大成就獲得諾貝爾物理學(xué)獎。 他提出了一個關(guān)于規(guī)模的理論。 特別是，威爾遜展示了不同尺度之間看似嚴格的障礙如何在所謂的臨界點附近被打破。 例如，當冰塊接近融化時，分子水平上發(fā)生的事情突然影響宏觀水平上發(fā)生的事情，反之亦然。 尺度之間的隔離被打破，所有尺度都有助于從冰到水的轉(zhuǎn)變。
威爾遜的研究產(chǎn)生了深遠的影響。 對于量子理論的標準模型物理學(xué)家成就，威爾遜揭示了尺度如何影響我們將測量的自然基本常數(shù)，更重要的是，揭示了原因。 在威爾遜進行研究之前，物理學(xué)家一直認為他們是在用方程玩某種數(shù)學(xué)游戲才能得到合理的結(jié)果。 威爾遜證明了事實并非如此。 相反，一切都是成比例的。 像萬有引力常數(shù)和精細結(jié)構(gòu)常數(shù)這樣的常數(shù)根本不是常數(shù)，而是在很大程度上取決于測量它們的尺度。
特別是，他表明物理方程在特定尺度上會崩潰，但在某些情況下你可以忽略較小尺度上發(fā)生的事情，因為你不理解也不知道發(fā)生了什么。 相反，您可以將一個尺度與稍小的相鄰尺度相關(guān)聯(lián)，并提出當實驗儀器檢測到越來越小的長度時自然常數(shù)如何從一個尺度變化到另一個尺度的公式。 規(guī)模變化。 這種由于歷史原因被無意義地稱為“重正化群論”的數(shù)學(xué)技術(shù)永遠改變了量子物理學(xué)，是過去 50 年來物理學(xué)中最重要的數(shù)學(xué)成就之一。
這并不是微觀層面上發(fā)生的唯一奇怪的事情。 科學(xué)家們已經(jīng)證明，如果尺度足夠小，時間實際上可以倒退一小段時間。 僅由幾個分子組成的機器可能會受益于這種奇怪的時間扭曲。 原因是熱力學(xué)第二定律控制著我們認為時間流動的方向，它是一個統(tǒng)計定律，并且像所有統(tǒng)計定律一樣，當樣本量變小時，它就會被違反。 在小范圍內(nèi)，違規(guī)行為變得越來越有可能，并且確實可以觀察到時間倒流。
在科技領(lǐng)域英語作文，雖然飛機使用類似于鳥類的固定翼，但在小范圍內(nèi)，這是行不通的。 較小的規(guī)模意味著更多的湍流，需要更多類似昆蟲的翅膀運動。 在尺寸較小的情況下，鞭狀鞭毛以奇怪的螺旋模式移動，推動單細胞生物前進，包括允許人類繁殖的精子細胞。
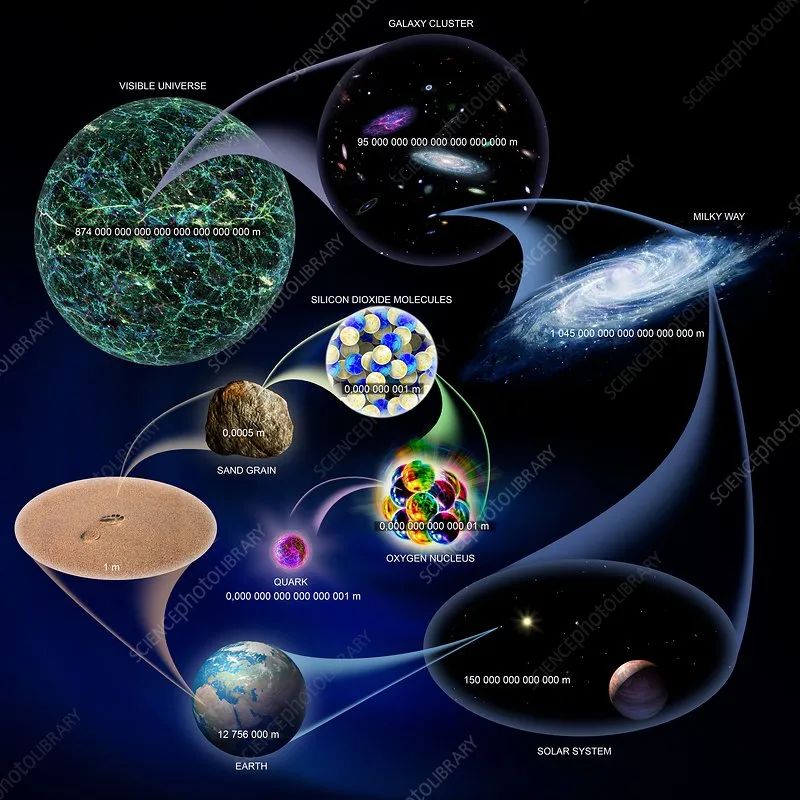
與此同時，在最大尺度上，宇宙變得像光滑的流體。 每個星系和超星系團就像數(shù)十億人中的一個分子。 雖然宇宙，即使在最大的尺度上，也有一些網(wǎng)狀結(jié)構(gòu)，但它在很大程度上平穩(wěn)地移動和膨脹。 然而，在數(shù)十億年前的某個時刻，我們所知的最大結(jié)構(gòu)，即可觀測宇宙的 460 億光年，比原子核還小。 在這個尺度上，宇宙與最微小的尺度發(fā)生碰撞，我們不知道此時會發(fā)生什么。 我們只知道當宇宙稍微大一點并且我們所知道的普通物理學(xué)出現(xiàn)時會發(fā)生什么。
關(guān)于尺度的有趣之處在于，在望遠鏡和顯微鏡被發(fā)明并變成科學(xué)儀器之前物理學(xué)家成就，這些東西甚至是不可見的。 伽利略圍繞這些儀器建立了業(yè)務(wù)，一度幾乎成為壟斷企業(yè)。 然而，他們還使用這些儀器來極大地擴展我們對最大和最小尺度上發(fā)生的事情的理解。 從木星的衛(wèi)星到一滴水，我們的世界開始向兩個方向擴展。
關(guān)鍵是，對于不同的尺度，我們通常使用不同的物理原理。 在星系和宇宙的尺度上，我們使用愛因斯坦的長方程。 其中沒有任何關(guān)于地球上生命多樣性的內(nèi)容，也沒有任何關(guān)于原子的內(nèi)容，因為這些都不重要。
同樣，在最小的尺度上，我們有量子物理學(xué)。 有人說所有物理都是量子的，但我們不用量子物理來討論洋流。 而且，盡管人們進行了許多嘗試，但將量子物理學(xué)應(yīng)用于恒星或宇宙尺度方面卻收效甚微。 唯一真正的例外可能是斯蒂芬·霍金關(guān)于黑洞熱力學(xué)、熵和霍金輻射的一些工作，它將兩者結(jié)合起來。 然而，其中大部分尚未得到證實。 對于大型恒星黑洞，量子效應(yīng)基本上是不可見的。 我們沒有制造微小黑洞的儀器，但我們可以通過研究證實大部分預(yù)測。 我們還沒有發(fā)現(xiàn)任何自然發(fā)生的原初黑洞（它們可能小到足以觀察到）。
事實上，每個尺度都有自己的物理現(xiàn)象，跨尺度的物理現(xiàn)象相當罕見。 唯一的例外可能是電磁力，但即使電磁力在與其他力結(jié)合時也會在最小的尺度上崩潰。
這就是威爾遜的研究既令人著迷又令人擔憂的地方，因為他表明，在這些臨界點，所有尺度都很重要。 這意味著，如果宇宙中的大尺度結(jié)構(gòu)現(xiàn)在或過去經(jīng)歷了臨界點，我們可能無法理解它們，具體取決于尺度有多大，除非我們有一個結(jié)合大尺度和小尺度的總體理論。
黑洞和奇異結(jié)構(gòu)可能是這些臨界點發(fā)揮作用的地方。 在這些情況下，我們使用愛因斯坦的物理學(xué)，但愛因斯坦的物理學(xué)忽略了微小的量子尺度。 為了理解這些關(guān)鍵現(xiàn)象，我們必須擁有包括愛因斯坦和量子尺度物理學(xué)的物理學(xué)。 我們不能忽視其中任何一個。
直接的解決方案是“量化”愛因斯坦的方程，但這被證明是困難的，沒有人能弄清楚如何做到這一點，因為愛因斯坦的理論只是大尺度上的“有效”理論，在任何其他尺度上都不起作用。 我們需要找到一種在所有尺度上都有效的“真實”引力理論。
這個理論是由一個名叫波利亞科夫的人發(fā)明的。 波利亞科夫方程確實適用于所有尺度。 波利亞科夫方程中也有與愛因斯坦的引力場非常相似的東西。 最近，數(shù)學(xué)家實際上已經(jīng)證明了它在二維中的工作原理。 他們花了四十年的時間才證明了這一點，而且只是在二維方面。 如果他們能在 4 個維度上做到這一點，他們可能就會有一個可行的理論。 無非就是弦理論。
另一個建議是，引力有其最小的尺度，實際上沒有什么比它更小的了。 畢竟，愛因斯坦方程確實告訴我們某物有多長。 這是一個“度量”場論。 重力改變物體的長度。 如果它可以確定這些事情，為什么它不簡單地告訴我們事情可以有多小呢？
在計算機中，我們在模擬任何事物時總是引入最小尺寸，因為計算機是有限的機器。 但對于大多數(shù)事物，最小尺寸會疊加在某些不假定具有最小尺寸的背景上。 對于重力來說，如果你確實假設(shè)了一個最小尺寸，它就不會疊加在任何東西上。 空間和時間中的每個點都沒有“位置”，因為要擁有一個位置，你必須有一些背景現(xiàn)實來與之比較。
這和這個想法很相似。 您必須根據(jù)每個點與其他點的關(guān)系來定義每個點。 事實上，這是這個時空理論中任何給定點的唯一定義特征。 它以某個最小距離連接到相鄰點。 這就是環(huán)量子引力。
還有一些理論試圖以某種方式消除規(guī)模問題。 例如，通過將重力轉(zhuǎn)化為第五維度。 這種量化并不會告訴你在最小尺度上會發(fā)生什么，它只是告訴你這些尺度應(yīng)該是可控的，因為引力在最小尺度上是確定性的，盡管是混亂的。 它還從根本上挑戰(zhàn)了量子物理學(xué)，將其納入愛因斯坦的廣義相對論中。
無論答案是什么，它都必須解決這一問題：當重力達到最小尺度時會發(fā)生什么？ 重力會改變嗎？ 量子物理學(xué)會改變嗎？ 現(xiàn)實就這樣停止了嗎？ 如果我們確實找到了正確的理論，我們?nèi)匀挥泻芏喙ぷ饕觯宰C明它與我們在最大尺度上看到的相符。
最近有人問，如果我們只能用有理數(shù)來衡量位置和時間呢？ 這對這個問題有幫助嗎？ 有理數(shù)是整數(shù)之比，并非所有數(shù)字都是有理數(shù)。 事實上，無理數(shù)比有理數(shù)多得多。 然而，生活中遇到的每一個數(shù)字都是有理數(shù)。 原因是我們根本無法處理具有無限個不重復(fù)數(shù)字的數(shù)字。 問題是：這能解決擴展問題嗎？
它不會解決問題。 有理數(shù)可以代表您選擇的任何比率。 人們對連續(xù)數(shù)感到困惑，但它們很少成為物理學(xué)中的真正問題。 通過使用限制和比例可以很容易地控制連續(xù)數(shù)字帶來的任何問題。 我認為非數(shù)學(xué)家只是害怕它們，因為當你處理連續(xù)數(shù)字時，你會失去離散數(shù)字的直觀性。 您必須考慮無限維的函數(shù)和運算符的空間。 真讓人頭暈。 但真正的問題不是連續(xù)性，而是規(guī)模。 這是一個關(guān)于數(shù)字無窮大的問題，而不是數(shù)字連續(xù)性的問題。 引入一個有限的宇宙，你可能會解決這個問題，但你必須回答這個問題：宇宙有多大或多小？
由于黑洞奇點尚無法測量，因此不可能知道真正的答案是什么。 也許有一天引力波探測器會告訴我們。 另一種可能性是，將引入一種新理論來解釋一些其他現(xiàn)象，例如暗物質(zhì)和暗能量，并且不存在與愛因斯坦相同的尺度問題。 無論解決方案是什么，它都需要在巨大和微小的尺度上發(fā)揮作用。