
幾何的學(xué)習(xí)一直是很多學(xué)生的難點(diǎn)和痛點(diǎn)。 一方面,幾何是中考、高考必修的熱門(mén)話題,非常重要。 另一方面,有些學(xué)生找不到幾何學(xué)習(xí)的竅門(mén),常常在這方面丟分。 例如,中考數(shù)學(xué)中,函數(shù)和幾何占整張?jiān)嚲淼?0%以上。 如果幾何學(xué)不透,那就告別重點(diǎn)高中吧。
近年來(lái),與等腰三角形相關(guān)的試題經(jīng)常出現(xiàn)在全國(guó)高中數(shù)學(xué)入學(xué)考試中等腰三角形公式,形式多樣,內(nèi)容新穎。 與等腰三角形相關(guān)的知識(shí)、定理、方法和技能是整個(gè)初中幾何的核心知識(shí)。 是中考出題老師設(shè)計(jì)新題型的典型素材。 常見(jiàn)的新題型有折疊式、網(wǎng)格式、剪紙式、展開(kāi)式、常規(guī)式等。 等,可以更好地考驗(yàn)學(xué)生的應(yīng)用意識(shí)和思維能力。
再加上等腰三角形的“不確定性”,也會(huì)產(chǎn)生一些分類(lèi)討論問(wèn)題。 在等腰三角形分類(lèi)的討論中,通過(guò)遞進(jìn)的問(wèn)題和條件設(shè)置,引導(dǎo)學(xué)生對(duì)邊、角、頂點(diǎn)以及更高條件進(jìn)行分類(lèi),幫助學(xué)生掌握分類(lèi)原理,體驗(yàn)分類(lèi)思想。
解決分類(lèi)討論相關(guān)的試題,最重要的是把握以下兩點(diǎn):
1、掌握分類(lèi)原則,即統(tǒng)一標(biāo)準(zhǔn),不重復(fù)、不遺漏,力求盡可能簡(jiǎn)單;
2.理解分類(lèi)的思想,就是不能確定就必須分類(lèi)。
以往的中考中,很多考生在處理等腰三角形相關(guān)的多解題時(shí),往往考慮不周,導(dǎo)致漏解、失分。

中考等腰三角形相關(guān)題、講解與分析1:
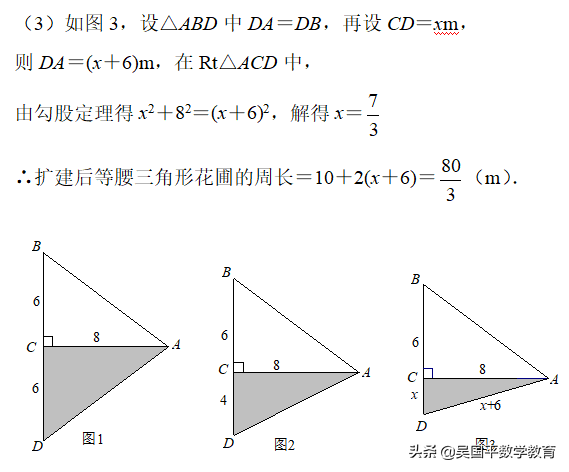
一家園藝公司翻新了一個(gè)直角三角形花壇。 測(cè)量?jī)蓚€(gè)直角邊的長(zhǎng)度分別為6m和8m。 現(xiàn)在我們要把它展開(kāi)成一個(gè)等腰三角形,展開(kāi)的部分是一個(gè)以8m為直角邊的直??角三角形。 求展開(kāi)的等腰三角形花園床的周長(zhǎng)。


測(cè)試點(diǎn)分析:
等腰三角形、直角三角形、鉤定理、分類(lèi)思想、設(shè)計(jì)問(wèn)題、分類(lèi)思想、畢達(dá)哥拉斯定理、設(shè)計(jì)問(wèn)題
題干分析:
原問(wèn)題沒(méi)有提供數(shù)字。 你需要畫(huà)一個(gè)符合問(wèn)題含義的圖形。 畫(huà)完圖可以看出,這道題其實(shí)涵蓋了三類(lèi)情況:一是把△ABC沿直線AC對(duì)折180°后,得到等腰三角形ABD,如圖1所示; 其次,將BC延伸到D點(diǎn),使CD=4,則BD=AB=10,得到等腰三角形ABD,如圖2所示; 第三,使斜邊AB的垂線交于BC的延長(zhǎng)線于D點(diǎn),則DA=DB,得到等腰三角形ABD,如圖3所示。首先制作滿足條件的圖形,然后根據(jù)畢達(dá)哥拉斯定理求解。
解決問(wèn)題的反思:
對(duì)于沒(méi)有繪圖的幾何問(wèn)題,往往需要根據(jù)問(wèn)題的含義繪制圖形,并結(jié)合已知條件和圖形分析來(lái)解決,這樣更容易找到解題思路。

?等腰三角形相關(guān)中考題講解分析2:
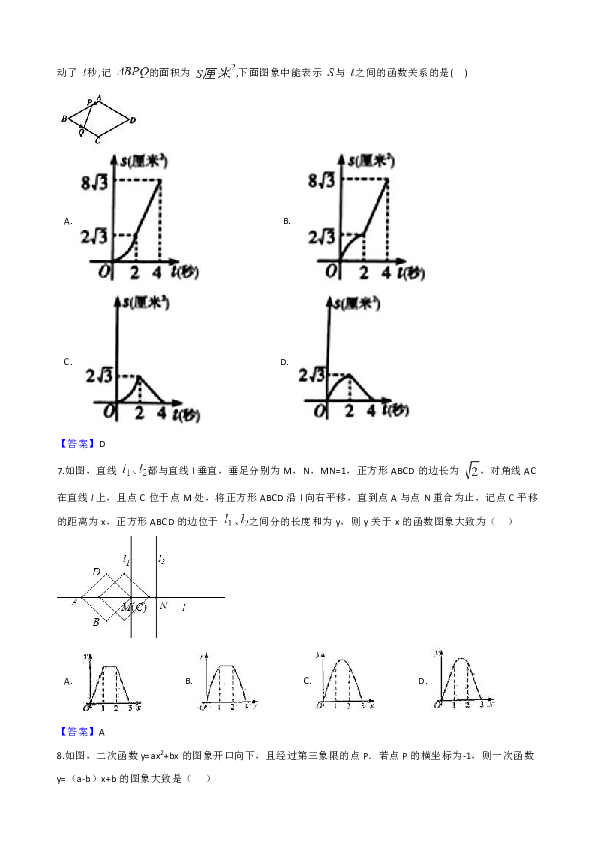
已知:如圖所示物理資源網(wǎng),O為坐標(biāo)原點(diǎn),四邊形OABC為矩形,A(10, 0),C(0, 4),D點(diǎn)為OA的中點(diǎn),P點(diǎn)在BC上移動(dòng),當(dāng)△ODP為腰圍 如果等腰三角形的長(zhǎng)度為5等腰三角形公式,則P點(diǎn)的坐標(biāo)為。


測(cè)試點(diǎn)分析:
矩形的屬性; 坐標(biāo)和圖形的屬性; 等腰三角形的性質(zhì); 數(shù)字和形狀的組合。
題干分析:
有三種情況:PD=OD(P在右邊)、PD=OD(P在左邊)、OP=OD。 根據(jù)題意畫(huà)圖,垂直于x軸畫(huà)PQ,找到直角三角形,根據(jù)勾股定理計(jì)算出OQ,然后根據(jù)圖寫(xiě)出P的坐標(biāo)。
解決問(wèn)題的反思:
這是一個(gè)結(jié)合了代數(shù)和幾何知識(shí)的開(kāi)放式問(wèn)題。 它全面考察了等腰三角形和畢達(dá)哥拉斯定理的應(yīng)用。 它對(duì)戰(zhàn)略和結(jié)果持開(kāi)放態(tài)度。 這類(lèi)問(wèn)題的解決方法是:將數(shù)字和形狀結(jié)合起來(lái),按照邏輯構(gòu)圖來(lái)解決問(wèn)題。
在學(xué)習(xí)等腰三角形的性質(zhì)和判定時(shí),分類(lèi)討論的思想尤為重要,希望大家認(rèn)真對(duì)待。
等腰三角形相關(guān)的綜合題具有探索性、開(kāi)放性、一定的挑戰(zhàn)性,分類(lèi)思維是解決問(wèn)題的常用思維方式。 有利于學(xué)生思維有序、嚴(yán)謹(jǐn)、靈活的培養(yǎng)和發(fā)展。 學(xué)生只有掌握了分類(lèi)的思維方法,才能在解決問(wèn)題時(shí)避免漏解。
