圖析兩平面鏡成像個(gè)數(shù)的規(guī)律
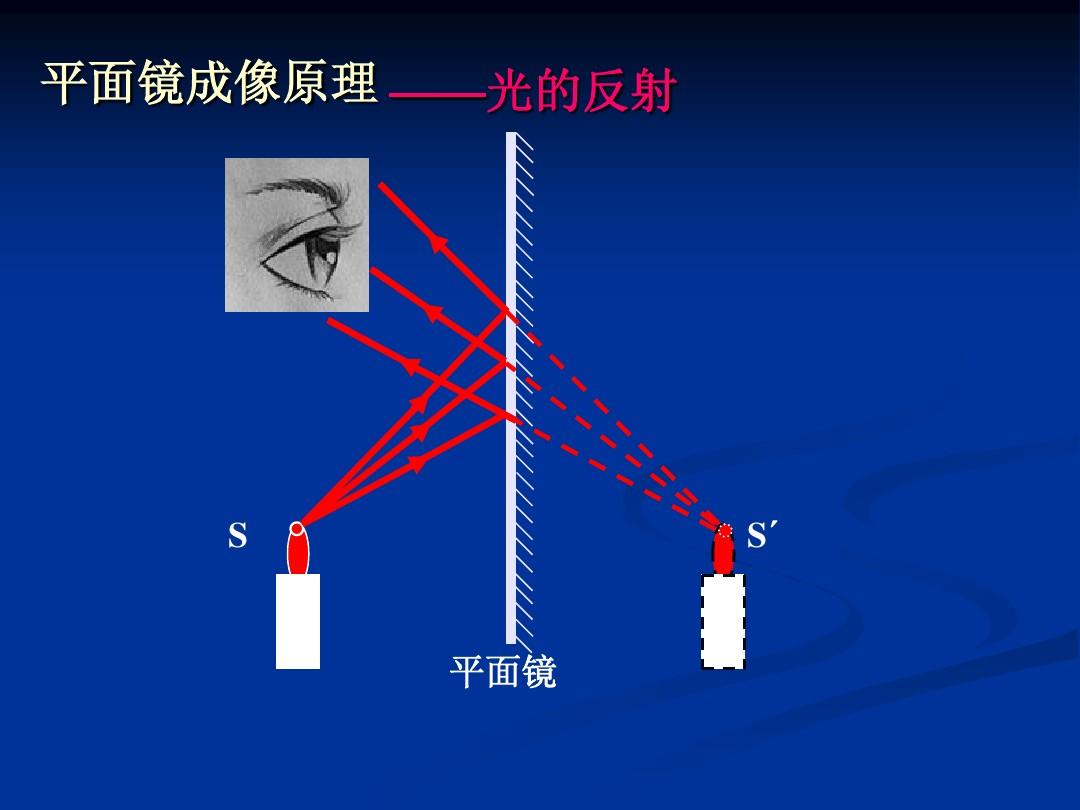
依據(jù)平面鏡成像原理,一個(gè)物體置于一塊平面鏡中只能成一個(gè)像,當(dāng)兩平面鏡構(gòu)成傾角不同時(shí),能成幾個(gè)像呢?關(guān)于角鏡成像個(gè)數(shù)估算的公式問題,有的刊物中的論文這樣敘述:這個(gè)問題“十分復(fù)雜”,“很難用一個(gè)簡單公式把物體成像的數(shù)量表示下來"。為了把復(fù)雜的問題簡單化,本文通過具體例子及作光路圖進(jìn)行簡易推理、歸納總結(jié)出兩平面鏡放置傾角不同時(shí)成像個(gè)數(shù)的規(guī)律,供你們參考。?例1:把點(diǎn)光源置于傾角為90°的兩塊平面鏡之間,
如圖1所示,能成幾個(gè)像??例析:本題畫圖法,借助平面鏡成像原理和像的對稱性兩種方式并作,可達(dá)到直觀、簡易性。依題意畫圖,點(diǎn)光源S置于垂直放置的兩平面鏡前,據(jù)光的反射定理或平面鏡成像規(guī)律,因?yàn)辄c(diǎn)光源S在兩平面鏡M1、M2中成像,見圖2中S1、,因?yàn)橐恍┕饩€分別射到M1、M2鏡面,反射后又分別射到M2、M1兩個(gè)鏡面上,被M1、M2兩個(gè)鏡面二次反射的光線是發(fā)散的(見①線、②線),但它們反向延長相交到一點(diǎn)S2,
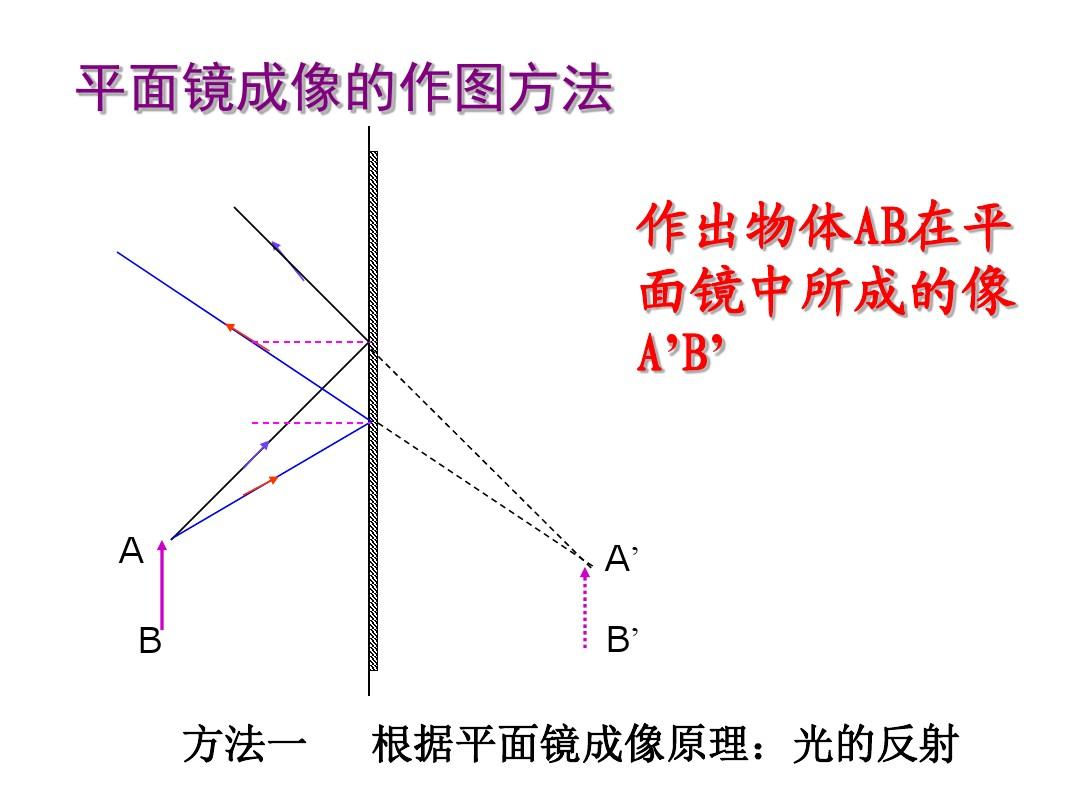
如圖2所示,這個(gè)點(diǎn)也是點(diǎn)光源的像,可見互成90°的兩平面鏡可成三個(gè)像,其中角頂?shù)囊粋€(gè)像S2是兩塊平面鏡所成的重合像。也可據(jù)平面鏡成像規(guī)律平面鏡成像原理圖片,像與物對鏡面互相對稱,把像與物聯(lián)接起:S→S1→S2→S3→S畫圖2中實(shí)線所示;S1是S在M1的像,S3是S在M2中的像,S2是S分別在M1、M2所成的重合像。從圖中很顯著看出物與像組成了一個(gè)正圓形,例2:在例1中,當(dāng)兩平面鏡之間的傾角改為60°時(shí)平面鏡成像原理圖片,點(diǎn)光源可成幾個(gè)像??例析1:?1。像的位置
如圖3所示,點(diǎn)光源S在平面鏡OM1和OM2之間,以兩鏡交點(diǎn)O為圓心,以OS為直徑作圓。據(jù)平面鏡成像規(guī)律,像與物對鏡面對稱:像S1,S5分別跟平面鏡OM2,OM1與點(diǎn)光源S對稱,S2與S3跟平面鏡OM1對稱,,所以S1,S2,S3,S4,S5也分布在以O點(diǎn)為圓心,,,其余每等分角內(nèi)均有一個(gè)像。
2.像的個(gè)數(shù)?據(jù)平面鏡成像規(guī)律,可作得點(diǎn)光源S在平面鏡OM1、OM2的兩個(gè)傾角之間可成5個(gè)像:即S1是S在OM2中的像,S5是S在OM1中的像,S4是S1在OM1的像,S2是S5在OM2中的像,其中角頂?shù)囊粋€(gè)像S3,是S分別在OM1,OM2兩鏡中所成的重合像,而S3重合像不能再在OM1,OM2中成像。?
例3按例2,當(dāng)平面鏡之間的傾角改為30°時(shí),點(diǎn)光源可成幾個(gè)像??例析:按例2方式畫圖1~4,從圖可知,該點(diǎn)光源可成11個(gè)像。其中角頂?shù)囊粋€(gè)像S6是M1、M2兩塊平面鏡所成的重合像。物與像可組成一個(gè)正十二邊形,除物點(diǎn)外,其余像點(diǎn)均分面在等分角內(nèi)。
從上述三例可看出,物與像之間組成了一幅對稱圖形,有直接相鄰的對稱,也有間接相鄰的對稱和軸對稱,,α表示兩平面鏡之間的傾角,則有:?n=■—1(0°≤α≤180°情況下組建)?上式是從三個(gè)特殊例子中總結(jié)下來的,并且360°均能被a整除得到奇數(shù),其重合像為1個(gè)。因而它只能適用于360°被整除的一系列傾角
