姓名
【知識點】
.正交分解法
Fx==Fsin/
將力沿兩個相互垂直的方向分解的方法稱為正交分解法。
(第 4 講力的正交分解和三角定律
姓名
【知識點】
.正交分解法
Fx==Fsin/
將力沿兩個相互垂直的方向分解的方法稱為正交分解法。
.正交分解法計算合力的步驟 (1)分析物體受力
(2)選擇和改進坐標系。 以公共點力的作用點為坐標原點,構建正交直角坐標系。
大量的力作用在坐標軸上,使所有力與坐標軸的傾角盡可能特殊
(3) 沿兩個坐標軸分解不在坐標軸上的力。 +y
(4) 將同一坐標軸上的向量合成c
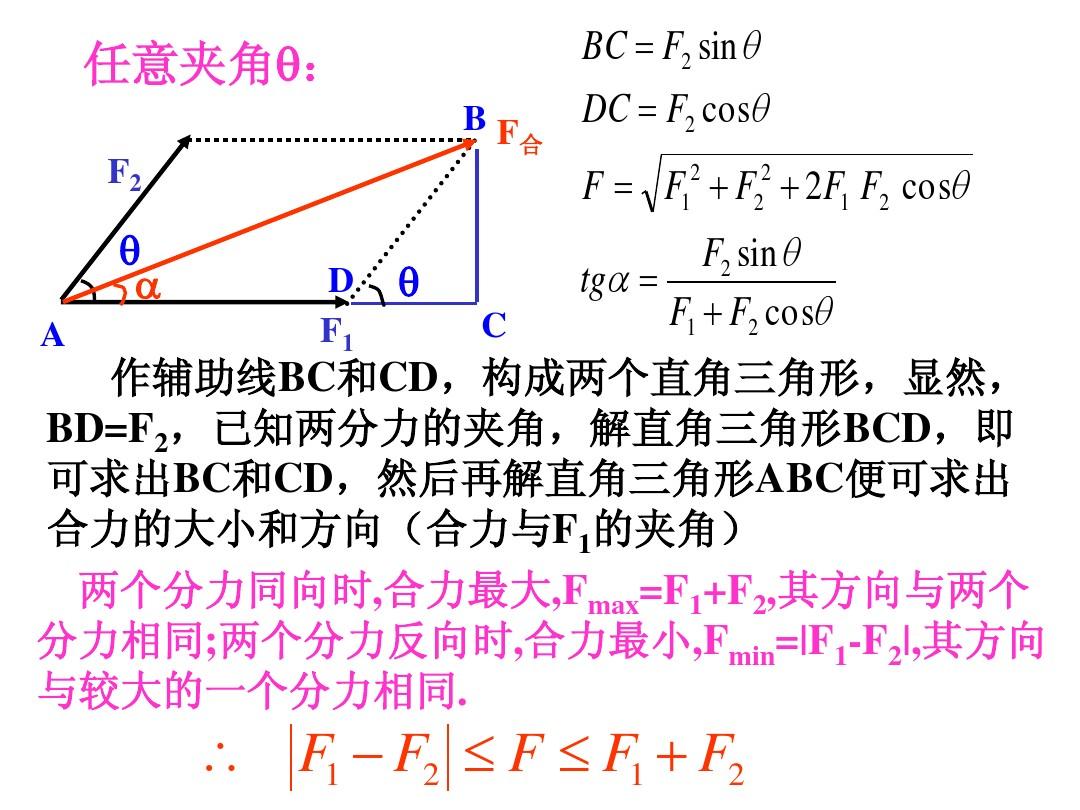
{Fx=修復+F2x=-
Fy=Fiy+F2y=+
從這個公式可以看出,力的數量越多力的正交分解怎么找角,這個方法就越方便。
(5)然后合成x軸方向的Fx和y軸方向的Fy。 此時兩個分力的傾斜角是一個特殊的角度
90°。 因此合力方向與x軸正方向的傾角為8=(Fy/Fx)
注:采用正交分解法求合力時,先將每個力分解為兩個不同坐標系的力,然后在同一個坐標系中按簡單的代數運算進行合成(相互成直角)方向或相反方向。 它在一個角度的多個力的合成中具有非常顯著的優勢。
采用正交分解法求合力,采用“欲合先分”的策略來降低計算難度,是求解問題的重要思路。
合力與分力之間的關系遵循平行四邊形規則。 根據平行四邊形的性質,對應邊平行且相等,即分力和
段,表示這兩個力合力的大小和方向
筆記:
解決相似度問題的步驟:
.物體受力分析
.繪制力矢量三角形和幾何三角形
. 由對應邊的比例關系計算出未知力
【典型案例】
例1:求正多邊形內五個力的合力
例2:如圖所示,細線的一端固定在A點,質量為m的物體掛在線的中點上,另一端B用手握住。
當AO與垂直方向、OB&水平方向成夾角時,AO、BO對O點的拉力分別為多少?
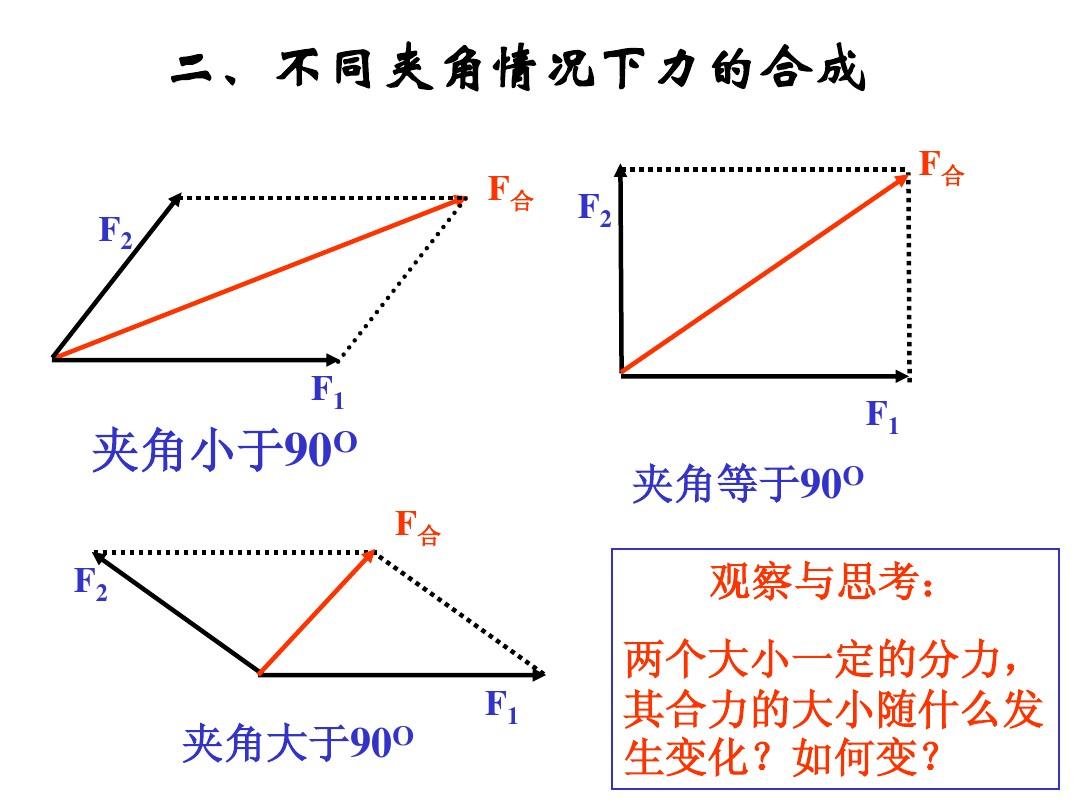
例3:如圖所示,力Fi、F2、F3、F4在同一平面內形成公共點力,其中Fi=20N>F2=20N,
F3=20.2N,F4
向。
20v^N,力之間的傾角已經在圖中標出,求這四個力合力的大小和平方
例4:如圖所示,一個拉力F作用在一個重量為G的物體上,使其沿水平地面勻速運動。 如果物體與地面接觸
動摩擦力的質數是,拉力最小時地面的傾角是多少?
,其中一個分力方向成30度角,試討論:
(1) 另一個分力的大小是多少?
(2)如果另一個分力的大小為2O/1^N,那么已知方向的分力大小是多少?
例6:如圖所示力的正交分解怎么找角,質量為m的小球被長度為L的輕繩掛起,靠在直徑為r的光滑半球上。 繩索掛點A到球面的最小距離為d。 (1) 求小球在繩子上的拉力和半球上的壓力。 (2)
如果 L 變短,繩子上的球的張力和半球上的壓力會發生什么變化?
[經典練習****br/>。 已知這兩個力的合力是
()
10N,其中一個分力與合力的傾角為37°。 , 那么另一個分力的大小是
b.
d.
不可能小
