

免費下載!
[!--downpath--]《極化恒方程在向量問題中的應用.docx》由會員分享,可在線閱讀,更多相關《極化恒方程在向量問題中的應用.docx(8頁典藏版)》請在三一文庫上搜索。
1、。極化恒方程在向量問題中的應用目標1:閱讀材料,了解極化恒方程的來歷過程,把握極化恒方程的兩種模式,并理解其幾何意義閱讀以下材料:引例:平行四邊形是表示向量乘法和加法的幾何模型。你能用向量方式證明:平行四邊形的對角線的平方和M等于兩條鄰邊平方和的兩倍.證明:不妨設ABa,ADb,則ACab,DBab,22222圖ba2abb(1)ba2abb(2)(1)(2)兩式相減得:AC2推論:定律:平行四邊形對角線的平方和等于兩條鄰邊平方和的兩倍.思索1:假如將前面(1)(2)兩式相加,能
2、得到哪些推論呢?ab1abab22極化恒方程ab4“和對角線”與“差對角線”平方差的1.幾何意義:向量的數目積表示為以這組向量為鄰邊的平行四邊形的4即:ab221ACDB(平行四邊形模式)A4思索:在圖1的三角形中(為的中點),此恒方程怎么表示呢?由于AC2AM,所以abAM目標2-1:把握用極化恒方程求數目積的值(三角形模式)4例1.(2012年廣西文15)在ABC中,M是BC的中點,AM3,BC10極化恒等式推導證明,則ABAC_.解:由于M是BC的中點,由極化恒方程得:21BC2=-16AB
3、ACAM=9-110044【小結】運用極化恒方程的三角形模式,關鍵在于取第三邊的中點,找到三角形的中線,再寫出極化恒方程。目標測量(2012上海文13改編)已知正圓形ABCD的周長為1,點E是AB邊上的動點,則DEDA的值為_.目標2-2:把握用極化恒方程求數目積的最值、范圍例(自編)已知正三角形ABC內接于直徑為的圓,點是圓O上的一個動點,2.2OP則的取值范圍是_.PAPB解:取AB的中點D,聯結CD,由于三角形ABC為正三角形,所以O為三角形ABC的重心,O在CD上,且,所以CD3,AB23又由極化恒方程得:
4、PA由于P在圓O上,所以當P在點C處時,|PD|max3當P在CO的延長線與圓O的交點處時,|PD|min1所以PAPB2,6【小結】涉及數目積的范圍或最值時,可以借助極化恒方程將多變量轉變為單變量,再用數形結合等方式求-可編輯更改-。出單變量的范圍、最值即可。目標測量1、矩形ABCD中,AB3,BC4,點M,N分別為邊BC,CD上的動點,且MN2,則AMAN的最小值是()A13B15C17D192、已知A,B,C是圓x2y21上互不相同的三個點,且ABAC,則ABAC
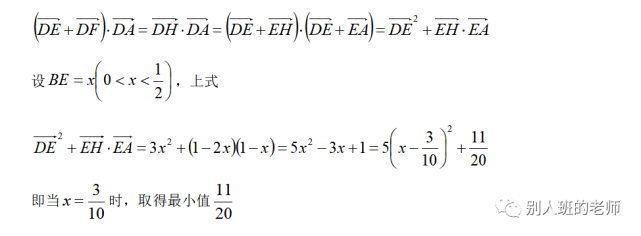
5、的最小值是3、已知ABC,AB7,AC8,BC9,P為平面ABC內一點,滿足PAPC7,則|PB|的取值范圍是.目標2-3:會用極化恒方程解決與數目積有關的綜合問題例3.(2013湖南理7)在ABC中,1P0是邊AB上一定點,滿足P0BAB,4且對于邊AB上任一點P,恒有PBPCP0BPC)0。則(A.ABC90B..ABACD.ACBC目標測量(2008四川理9)已知a,b是平面內2個相互垂直的單位向量,若向量c滿足1、c)(bc)0,則c的最大值是()(aA.1B.2C.2
6、D.222、2016年廣東如圖,在D中,是的中點,,是上的兩個三等分點,CA4,BFCF1,則BECE的值是.3、2014年廣東如圖在平行四邊形ABCD中,已知AB8,AD5,CP3PD,APBP2,則ABAD的值是.課后檢查1.在ABC中,BAC60若AB2,BC3,D在線段AC上運動,DBDA的最小值為2.已知AB是圓O的半徑,AB長為2,C是圓O上異于A,B的一點,P是圓O所在平面上任意一點,則的最小值為()A.1B.1C.1D.14323在ABC
7、中,AB3,AC4,BAC60,若P是ABC所在平面內一點,且AP2,則PBPC的最大值為4在RtABC,ACBC2,已知點P是ABC內一點,則PC(PAPB)的最小值是.5.已知A、B是單位圓上的兩點,O為圓心,且,MN是圓O的一條半徑,點C在圓內,且滿足OCOA(1)OB(01),則CMCN的取值范圍是()A1,1B1,1C3,0D1,0246.正ABC周長等于3,點P在其外接圓上運動,則APPB的取值范圍是()A.3,3B.3,1C.1,3D.1,在銳角ABC中,已知B極化恒等式推導證明,ABAC2,則ABAC的取值范圍是32,MN是它內切球的一條弦(把球面上任意8、正方體ABCD-D1的棱長為2個點之間的線段成為球-可編輯更改-。的弦),P為正方體表面上的動點,當弦MN最長時,PMPN的最大值為-可編輯更改-。歡迎您的下載,資料僅供參考!旨在為企業和個人提供協議合同,企劃案計劃書,學習講義等等構筑全網一站式需求-可編輯更改-