1、輕桿模型的受力問題
共點力達到平衡狀況的問題里頭,經常會出現“輕繩(此繩重量忽略不計)、輕桿(這桿重量不計)以及輕彈簧(該彈簧質量不計)”這樣的表述,針對這些我們得格外留意。里頭有不少同學,對于輕桿施加力或者承受力存在誤解情況,覺得輕桿所承受的力或者它施加于其他物體之上的力必定沿著輕桿的方向,然而實際情況并非是這樣的。就如同圖1所展示的那樣,輕桿的某一端能夠圍繞O點出現轉動現象,另一端A系在了一條處于水平方向的繩子上面,有一個重物懸掛在桿的中點B位置上。對輕桿進行受力分析,能發現輕桿受到繩拉力F1,還受到豎直繩子的拉力T,包括地面對它的作用力F2,這三個力構成共點力。從圖2能夠瞧出,輕桿兩頭受力的方向都并非沿著桿的方向。
判斷輕桿所受的力是沿沿桿的方向的方法:
倘若輕桿除了兩端之外,未有受到跟桿存在夾角的外力的作用,這就是講,針對于輕桿而言,要是僅有兩端受力,那么桿兩端所遭受到的一個力(或者幾個力的合力)的方向必然是沿著桿的方向的。
照圖3所示,那不計重力的輕桿OP,能夠以O點作為圓心所在之處,于豎直平面之內自由自在地轉動。P端懸掛著一個重物,另外呢,還用一根輕繩經由滑輪系住該端高中物理桿的受力分析,在F這樣一個情形之下,當OP和豎直方向所形成的夾角α一點兒一點兒緩慢增大的時候(0 )。
A.恒定不變
B.逐漸增大
C.逐漸減小
D.先增大后減小
圖3
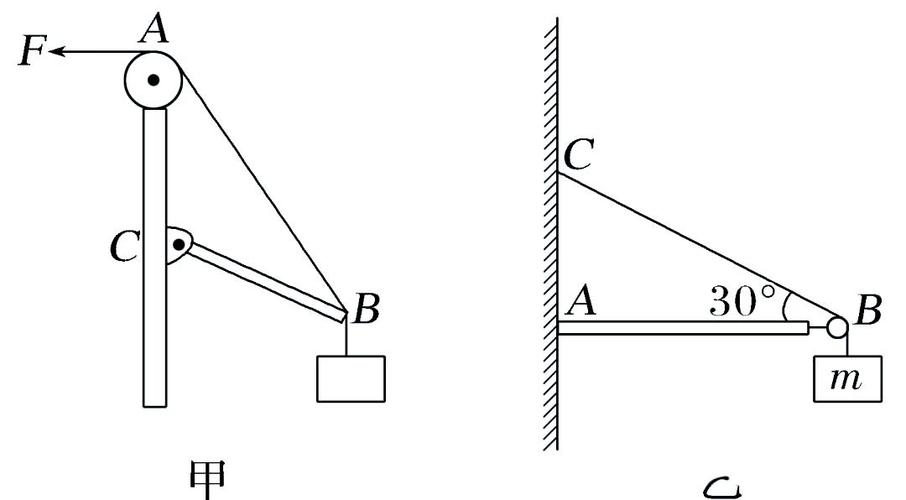
解答本題時,應先明確,輕桿于P點所受的T1、T2的合力必定沿桿的方向,此為解題關鍵所在。本題之中呢,要是合力F不沿輕桿方向,那么輕桿在力F力矩作用下會發生轉動,桿便不可能處于平衡狀態了。
在本題之中,輕桿僅僅兩端受力,于是輕桿于P點所受到的T1,以及T2的合力F必然沿著桿的方向,就如同4圖所呈現的那樣。
圖4
由三角形相似可知:
,可得:
即本題的答案為A。
2、非輕質桿的受力及平衡問題
所謂的非輕質桿,指的是桿自身的重力不能夠被忽略。在處理非輕質桿平衡問題之際,一般會采用三力匯交原理和力矩的相關知識來進行解答。所謂的三力匯交原理,是說一個物體要是受到三個并非平行的力作用進而處于平衡狀態,那么這三個力必定作用在物體的同一個點上,或者這三個力的作用線肯定會相交于同一個點。非輕質桿在三個非平行力作用下的平衡問題,是共點力平衡的典型模型中的一個,運用三力匯交原理去解決共點力平衡,是一種經常會用到的方法。在此,必須明確指出,并非,輕質桿當中的三力,并非一定就是三個力,而是,三個作用點。某些,作用于同一個點的兩個力,能夠用,一個等效力高中物理桿的受力分析,去進行取代。
當運用三力匯交原理來求解非輕質桿的具體問題之際,首先需要去判斷是不是屬于三個非平行力的平衡問題,這可是個難點,并且還是關鍵所在。要是能夠得出肯定的判斷結果,那便把三個力在不改變各力方向的情況下,移至匯交點上,接著再借助平衡條件來建立方程進行求解。
存在大量關于桿的情形,這種情形是桿處于在三個力作用下的平衡問題里,其中最為常見的模型呈現出來的狀況是兩個力是已知的,而第三個力是未知的。當處理這類問題之際,首要的步驟應當是把已知的兩個力的交點找尋出來,接著依據三力匯交原理將另一個力的方向確定出來,后續的問題便容易解決了。
有這樣一個情況,例2當中呢,有著重力為G的均質桿,其一端它能夠繞著O點進行轉動,另一端呢是拴在一條處于水平狀態的繩子上,此時這個桿與水平面形成了α角,就如同圖5所示展示的樣子。已知呢,繩子之中的張力大小是T,那么要去求O點對于桿所產生的作用力 。

圖5
剖析:此題目依循三力匯交原理拿來分析(就像圖6所展示那般),能夠輕而易舉地明確出O點針對桿的作用力的方向呢,如此一來便會讓問題變得簡單清晰起來。除此之外,這道題目也能夠繪制出繩子的拉力T、桿的重力G、O點的作用力這么三個力的矢量所構成的矢量三角形,憑借矢量三角形去求解 。

圖6
展開剖析:選取均質的桿當作要研究的對象,桿承受三個外力施加作用,具體這些力也就是重力 G,還有繩子所給予的拉力 T,以及 O 點施予的作用力量 F,其受力的圖示呈現如同圖 7 所直接顯示似的,鑒于桿正置身于平衡的狀態情形下物業經理人,因而這三個力的作用線路必然會交匯于同一個特定的點之上。

圖7
由圖6,運用平衡條件得:


