升入高一后的首個國慶節,僅僅學習了一個月的高中階段物理課程,便出現了好多人難以跟上進度的狀況。
回想初中階段以及中考那會兒,有誰的物理貝語網校,不是能超過九十分鐘以上才結束的,考到一百分或許也并不讓人覺得稀奇呢。
到了高中,一次測驗,怎么就都不一樣了呢?
最大的問題應該是學習方法不對。
我們這兒的學生,大多都很努力,喜好背誦,鐘情代數式,熱衷于計算,即便結果已然呈現,他依舊要去算,不算就心里不踏實,是典型的那種體力勞動者。
當然,學習高中物理背和計算,這是需要的,但更需要的是思考。
學習高中物理,你需要從體力勞動者轉變為腦力勞動者。
學習高中物理,得必修一者得天下。
我們有必要來看看高中物理必修一到底講了些什么。
第一章 運動的描述

運動的描述,主要講了三個方法。
第一個是理想化模型法。

于物理學里頭,把突出問題的關鍵要素,對次要要素予以忽略,構建起趨向理想的某類物理模型,并且拿此當作探討范疇的方法,于實踐進程里常按此開展探究舉措。質點這一具備著理想特性的 model 即是該種辦法在實際例子里的具體運用 。
第二個是極限的思想方法。

第三個是數形結合的思想方法。


在解決實際問題時,時間軸可以更直觀清晰的表達時刻與時間。

在位移-時間圖像里頭,存在著兩點之間的連線初中物理是什么,其斜率所代表的乃是相應時間范圍之內的平均速度,而在圖像上某一個點處的切線,該切線的斜率所表示的則是對應時刻的瞬時速度。

速度-時間圖像上,某點切線的斜率表示對應時刻的加速度。
第二章 勻變速直線運動的研究

勻變速直線運動的研究,主要是講一條直線和一個方法。
一條直線,就是速度-時間圖線。

勻變速直線運動存在相關問題,不是所有問題,僅靠平均速度加上速度-時間的圖像初中物理是什么,是沒辦法迅速解決的,沒有辦法快速解決的。
借助勻變速直線運動的兩個基本關系式,即勻變速直線運動的速度與時間的關系式,以及勻變速直線運動位移與時間的關系式,這二者均可由速度-時間圖像推導得出。
至于勻變速直線運動的別的公式,或者是推論,是能夠由這兩個基礎的關系式給推斷出來的。
自由落體運動,是一種運動,它在本質上屬于勻變速直線運動,并非是那種獨立存在的知識,豎直上拋運動同樣如此,也是本質上為勻變速直線運動,不是獨立知識,而勻變速直線運動的規律以及推論,對于它們都是適用的。
當然,勻變速直線運動位移與時間的關系式,還借助了微元法。
一個方法,就是微元法。
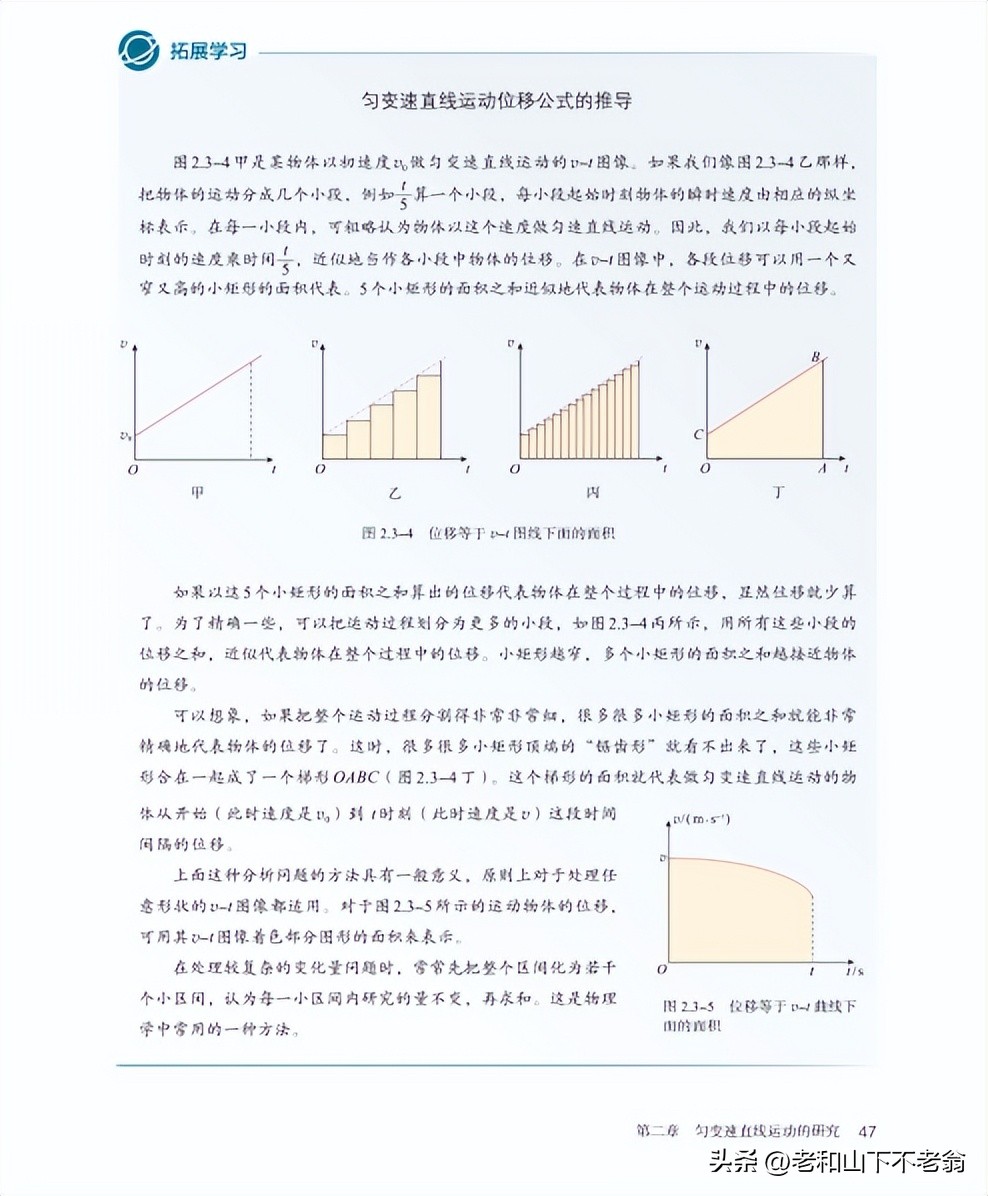
微元法,乃是高中階段用于解決變量累積問題的方式,往后諸如變力做功、變力的沖量這類問題,均能夠運用微元法予以解決。學習,應當學會方法的遷移。.
第三章 相互作用-力

有關相互作用的力,著重闡述的是矢量的合成法則,其中三角形的應用特別關鍵 。

解決三力平衡這個問題的時候,那是和三角形有關的問題,要運用到許多初中階段平面幾何方面的相關知識,還有相關方法。
如果物體受力多于三個怎么辦?
先合成其中幾個力,最終總可以變成三力平衡問題。
第四章 運動和力的關系

牛頓第二定律,它所闡述的是運動和力之間的關聯,用數學形式呈現為三個字母一個等號,即F=ma 。
將記住力視作合外力,把第二章知識與第三章知識綜合運用起來,這樣做就沒多大問題了 。
要是打算去考量某個方向上的加速度,于構建坐標系來實施力的分解之際,必然得把坐標系的其中一個軸順著加速度方向,這是由于如此這般去構建坐標系,能夠切實讓處于垂直于加速度方向的合外力變為0,進而把問題予以簡化 。
運動和力的關系,還講了一種方法,控制變量法。

關于超重和失重。超重,加速度向上,失重,加速度向下。

大家伙兒能夠去參看一下我所發布的那本名為《高中物理一招破之破選擇題》的東西里的相關練習 。
祝各位都能擁有好運,我所能做的也就是祝各位都能擁有好運了,到底能不能掌握高中階段的物理知識,就全看你自身的運氣和機遇怎樣了。
