

頁碼………………………………………………………………名校名師推薦……………………………………………… ……第 1 頁 ( 15) 萬有引力定律及其應用【A 級 - 做題熟練快速保分】 1.(2018·上海考試)關于萬有引力定律,下列哪項表述正確的是( )A。 牛頓提出萬有引力定律,并確定了萬有引力常數的值 B.萬有引力定律只適用于天體之間 C.萬有引力的發現揭示了自然界相互作用的基本規律 D.地球作橢圓運動繞太陽公轉,太陽在近日點和遠日點所施加的引力大小相同。 分析:選C。牛頓提出了萬有引力定律,卡文迪什確定了萬有引力常數的值。 萬有引力定律適用于任何物體。 兩者之間,萬有引力的發現揭示了自然界的基本相互作用規律。 選項A、B錯誤,C選項正確。 地球繞太陽公轉,太陽引力的大小在近日點和遠日點是不同的。 是的,D選項錯誤。 2、近年來,人類發射的多顆火星探測器陸續登陸火星,令人興奮的科學研究正在進行中,為我們未來登陸火星、開發利用火星資源奠定了堅實的基礎。 如果火星探測器繞火星作“近地”勻速圓周運動,測量到的該運動周期為T,則火星平均密度ρ的表達式為(k為某個常數) ( ) A. ρ =kTB. ρ=eq f(k,T)C. ρ=kT2 D. ρ=eq f(k,T2) 分析:選D。當火星探測器繞火星軌道做“近地”勻速圓周運動時,Geq f(Mm,R2)=meq f( 4π2,T2)R,且M =eq f(4,3)πR3·ρ,可得ρ=eq f(3π,GT2)=eq f(k,T2),所以只有D是正確的。
★3. (2017·浙江四月精選)如圖所示,假設行星繞太陽的運動是勻速圓周運動,金星本身的半徑是火星的n倍,質量是火星的k倍。 不考慮行星自轉的影響,則( )A。 金星表面的引力加速度是火星 B 的 eq f(k,n) 倍。金星的“第一宇宙速度”是火星 C 的 eq r(f(k,n)) 倍。金星繞太陽運動的加速度比火星D小。金星繞太陽運動的周期比火星大。 分析:選擇B,由Geq f(Mm, R2)=mg,得g=eq f(GM, R2)。 可見eq f(g gold, g fire) = eq f(k,n2),選項A錯誤; 由 Geq f(Mm,R2)=meq f(v2,R),得 v= eq r(f(GM,R)),可見 eq f( v gold, v fire ) = eq r(f(k,n)),選項B正確; 由Geq f(Mm,r2)=ma,我們得到a=eq f(GM,r2),可見距離越遠,加速度越小,而eq f(r3, T2) = c,可見距離越遠,周期越大,故C、D選項均錯誤。 4. [多選](2016·海南高考)通過觀測冥王星的衛星,可以計算出冥王星的質量。 假設衛星繞冥王星做勻速圓周運動,除了引力常數外,至少還需要兩個物理量來計算冥王星的質量。 這兩個物理量可以是( )A。 衛星速度和角速度 B. 衛星的質量和軌道半徑 C. 衛星的質量和角速度 D. 衛星運行周期和軌道半徑分析:選擇AD。 根據線速度和角速度,可求出半徑r=eq f(v,ω)。 根據萬有引力提供的向心力,有eq f(GMm,r2)=meq f (v2,r),可得M=eq f(v3,Gω),故選項A正確; 由于衛星的質量m可以減小,選項B、C錯誤; 如果我們知道衛星的運行周期和軌道半徑 ,則由 eq f(GMm,r2)=meq blc(rc)(avs4alco1(f(2π,T) ))2r,得M=eq f(4π2r3,GT2),故選項D正確。
5.(2018·廣州勘測)“嫦娥五號”探測器預計2018年發射,將自動完成月表樣本采集,然后從月球起飛返回地球,帶回月面樣本約2公斤月球樣本。 一位學生從上面得到了一些信息。 如表中數據所示,地球與月球的密度之比為 () 地球與月球的半徑之比 4 地球表面與月球表面的重力加速度之比 6A 。 eq f(2,3) B. eq f(3,2)C. 4 D. 6 分析:選B。在地球表面,重力等于萬有引力,所以mg=Geq f(Mm,R2)。 解為M=eq f(gR2,G),故地球密度ρ=eq f(M, V)=eq f(f(gR2,G),f(4,3) πR3)=eq f(3g,4πGR)。 同理,月球的密度ρ0=eqf(3g0,4πGR0)。 因此,地球和月球的密度之比eq f(ρ,ρ0)=eq f(gR0,g0R)=eq f(3,2),B是正確的。 6、如圖所示,取一個半徑為R,質量為M的均勻大球,沿直徑挖出兩個半徑為大球一半的小球,將其中一個放在球外,抵住大球。 同時,如果小球的中心、球外的小球的中心和大球的中心在一條直線上,則大球其余部分之間的萬有引力大小小球與小球外的小球的質量近似為(已知萬有引力常數為G)( )A。 0.01 eq f(GM2,R2) B. 0.02 eq f(GM2,R2)C. 0.05eq f(GM2,R2) D. 0.04eq f(GM2,R2) 分析:選D。由題可知,挖出的球的半徑為eq f(R,2),質量為eq f(M,8),所以沒有挖出來。 小球前面的大球對球外小球的引力大小為 F=Geq f(M×f(M,8),blc(rc) (avs4alco1( R+f(R,2)))2)=eq f(GM2,18R2),將挖出的其中一個球填入原來的位置,然后填入兩個球之間的距離左邊原位球和外側球 萬有引力為 F1=Geq f(f(M,8)×f(M,8),?2R?2)=eq f(GM2,256R2) ,將小球原來的位置填入球的右側和球外 小球的重力為 F2=Geq f(f(M,8)×f(M,8),R2)=等式 f(GM2,64R2)。 大球的剩余部分對球外的小球施加力。 萬有引力的大小為F3=F-F1-F2≈0.04eq f(GM2,R2)。 選項D正確。
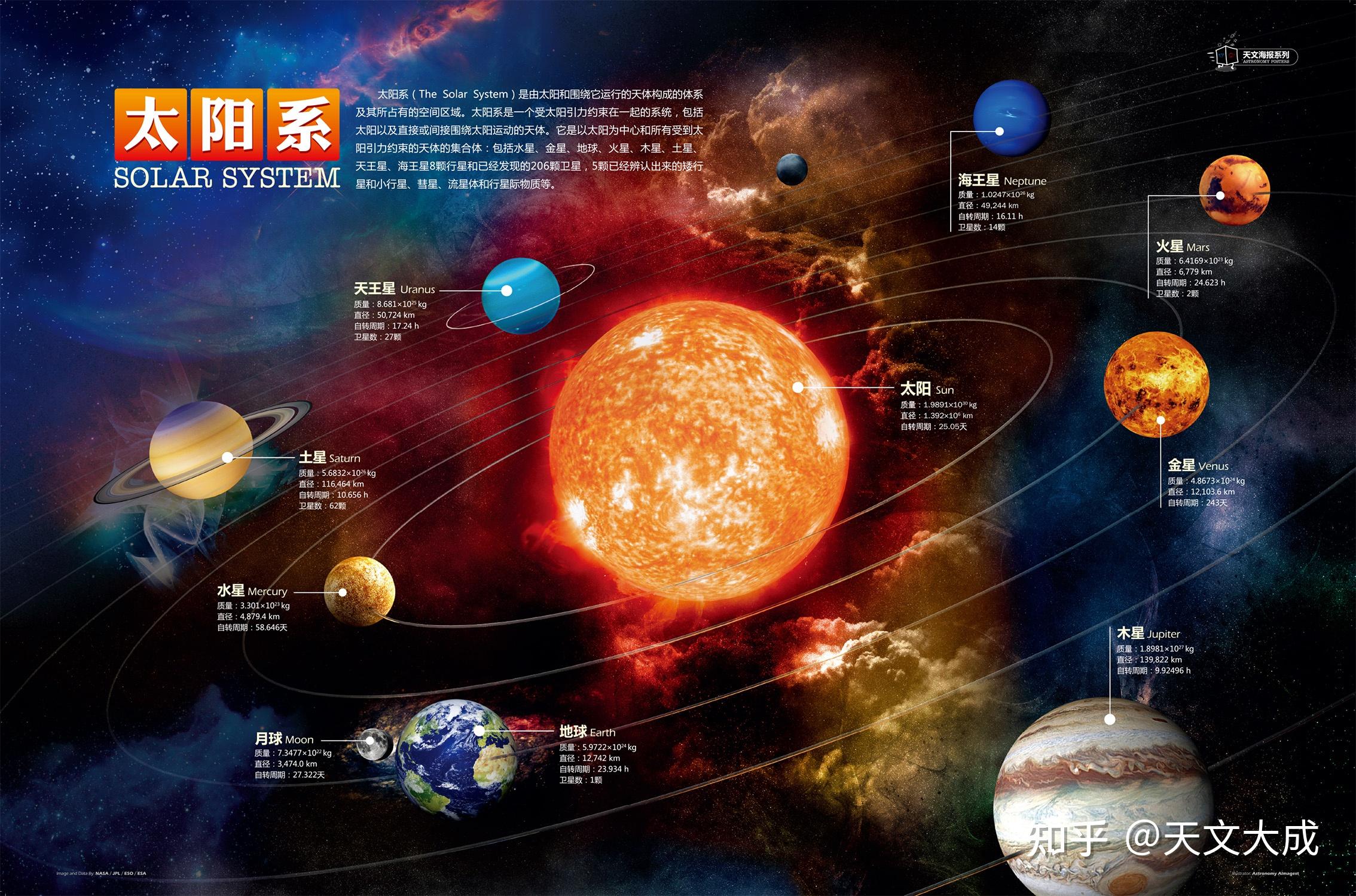
7.(2018·盤錦模擬)兩顆互不影響的行星P1和P2有一顆近地衛星S1和S2圍繞它們做勻速圓周運動。 圖中,縱軸表示行星周圍空間某一位置的重力加速度a,橫軸表示某一位置到行星中心的平方距離r的倒數。 a-eq f(1,r2)關系如圖所示。 衛星S1和S2的重力加速度大小為a0。 那么( )A。 S1的質量大于S2 B. P1的質量大于P2 C. P1的第一宇宙速度小于P2 D. P1的平均密度大于P2分析:選B。萬有引力為向心力,故Geq f(Mm,r2)=ma。 解為a=GMeq f(1,r2),所以圖像的斜率k=GM,因為G是常數,M代表行星的質量,斜率越大,行星的質量越大。 因此,P1的質量大于P2的質量。 由于計算過程中可以減少衛星的質量,因此無法判斷衛星的質量關系。 A錯誤,B正確; 由于這兩顆衛星都是近地衛星,因此它們的軌道半徑可以認為等于行星半徑。 根據第一宇宙速度公式 v=eq r(gR),我們可以得到 v=eq r(a0R) ,從標題圖可以看出,當兩個加速度均為 a0 時,P2 的半徑小于P1 的第一宇宙速度大于 P2 的第一宇宙速度,C 錯誤; 行星密度 ρ = eq f(M ,V)=eq f(M,f(4,3)πR3)=eq f(f(a0R2,G),f(4,3 )πR3)=eq f(3a0,4πGR) ,因此行星半徑越大,密度越小,因此P1的平均密度比P2的平均密度小,D誤差。
8、如圖所示,A、B是兩顆繞地球勻速圓周運動的衛星。 同等時間內兩顆衛星A、B的連線與地心所掃過的面積之比為k,不包括A、B。兩顆衛星之間的引力,則兩顆衛星的周期之比衛星 A 和 B 是 ( )A。 k3 B. k2C。 kD. keq f(2,3) 分析:選擇A,假設衛星繞地球做圓周運動的半徑為r,周期為T萬有引力定律及其應用,則t時間內與地心連線所掃過的面積則 S=eq f(t ,T)πr2,即 eq f (SA, SB) = eq f (rA2TB, rB2TA) = k。 根據開普勒第三定律 eq f (rA3, TA2) = eq f (rB3, TB2 ),聯立解為 eq f (TA, TB) = k3,A 正確。 9.(2018·寶雞一墨)宇航員在某顆行星上進行了如下實驗,檢測其自轉周期:在該行星的兩極,用彈簧秤測量質量為F的重物的重力,當在赤道處測量,重量施加的重力為F'。 他還發現探測器繞行星表面做勻速圓周運動的周期為T。假設行星可以看成一個質量分布均勻的球體,則它的自轉周期為( )A。 Teq r(avs4al(f(F′,F))) B. Teq r(f(F,F′))C. T eq r(avs4al(f(F-F′,F))) D. T eq r(f(F,FF′)) 分析:選D,假設質量行星和探測器在兩極分別為 m 和 m′,有: Geq f(Mm,R2)=F,在赤道有: Geq f(Mm,R2)-F′=MReq f( 4π2,T 來自 2)。 探測器繞行星表面勻速圓周運動的周期為T,則有: Geq f(mm ′,R2)=m′ Req f(4π2,T2); 結合以上三個方程,我們得到 T = Teq r(f(F,FF′))。
因此,D正確,A、B、C錯誤。 10.(2018·東北三省四市一個模型)開普勒第三定律規定:所有行星軌道半長軸的立方與其公轉周期的平方之比相等。 該定律適用于所有具有中心天體的引力系統。 如圖所示,嫦娥三號探月衛星繞月球運行一條半徑為r、周期為T的圓形軌道I,月球半徑為R,引力常數為G。在某一時刻嫦娥三號衛星在A點變軌進入橢圓軌道II,降落在月球表面B點。 A、O、B 三點在一條直線上。 求:(1)月球的密度; (2) 進入軌道 II 所需的時間。 分析: (1) 萬有引力作為向心力: eq f(GMm,r2)=meq blc(rc)(avs4alco1(f(2π,T)) ))2r ,解為 M=eq f(4π2r3,GT2) 月球的密度: ρ=eq f(M,f(4,3)πR3),解為 ρ=eq f( 3πr3,GT2R3)。 (2) 橢圓軌道的半長軸:a=eq f(R+r,2),假設橢圓軌道的運行周期為T1,根據開普勒第三定律:eq f(a3, T12)=eq f(r3,T2),在軌道II上運行的時間為t=eq f(T1,2),解為t=eq f(?R+r?T,4r) eq r(f(R+r, 2r))。
答案: (1)eq f(3πr3,GT2R3) (2)eq f(?R+r?T,4r) eq r(f(R+r,2r))[B級 - 穩定準確地做高題】★11. 已知質量為 m 的物體與北極和赤道靜止地面之間的壓力差為 ΔN。 假設地球是一個質量分布均勻的球體,半徑為R,則地球自轉周期為( )A。 T=2π eq r(f(mR,ΔN)) B. T=2π eq r(f(ΔN,mR))C. T=2π eq r(f(mΔN,R)) D. T=2π eq r(f(R,mΔN)) 分析:選A,在北極,物體所受的萬有引力F等于支撐力N。在赤道處,F-N=ΔN=mReq blc (rc)(avs4alco1(f(2π,T)))2萬有引力定律及其應用,解為 T=2π eq r(f(mR,ΔN)),A 正確。 ★12. (2018·商丘模擬)地質勘探發現某區域地表重力加速度發生明顯變化,懷疑地下存在空洞區域。 進一步探測發現,地面P點正下方的球形空腔區域儲存有天然氣,如圖所示。 假設該地區巖石分布均勻,密度為ρ,則天然氣的密度遠小于ρ,可以忽略不計。 如果沒有這樣的空腔,則地球表面的法向重力加速度為g; 由于空腔的存在,測得P點重力加速度為kg(k