

眾所周知,在高中各學科教學中,物理與數學聯系緊密,物理思維與數學思維也相通。例如極限思維方法、微分思維方法、等價思維方法等思維方法在數學和物理學中被廣泛運用。在高中物理的學習和解決問題的過程中,有很多定量的推導、定性的分析、證明和計算,這些都需要強大的數學工具。 然而在物理學習中,經常會發現學生沒有學到必學的數學知識,比如直線的斜率,弧長公式,弧度角,正弦定理,余弦定理……而高中數學中有些知識是建立在物理概念和規律之上的,比如遵循平行四邊形法則或三角形法則的矢量的加減運算高中物理的三角函數知識,極限的知識,變化率的知識,甚至導數和積分的知識等等,都是在物理學完了矢量的合成與分解(平行四邊形法則或三角形法則)、瞬時速度與瞬時加速度(速度變化率),速度圖中的位移之后才學到的。可以說,物理離不開數學,數學離不開物理。今天,本文就給大家提供一些學習高中物理必備的數學知識,希望對大家有所幫助和啟發。
1. 線性函數的圖形和斜率
函數y=kx+b(k、b均為常數)是一個線性函數,其圖像是一條直線,k稱為直線的斜率,反映直線傾斜的程度(注意,初中并沒有系統地講授這些內容)。
數學上,k=tanθ,其中θ是直線與x軸正方向的夾角。但在物理學上,我們只能說k與tanθ成正比高中物理的三角函數知識,即k∝tanθ。
2.特殊角的三角函數值、正弦定理與余弦定理
熟悉0°、30°、37°、45°、53°、60°、90°、180°角的三角函數值:
°=0,°=-1,°=-1,°=0。
sin37°=cos53°=0.6,cos37°=sin53°=0.8
sin(90°±θ)=cosθ,cos(90°-θ)=sinθ,cos(90°+θ)=-sinθ。
對于任意三角形ΔABC,a、b、c 為邊長:
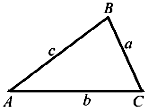
正弦定理:
余弦定理:c2=a2+b2-,a2=b2+c2-,b2=a2+c2-。
3. 弧度、周長和弧長公式的角度表達
在圓中,圓心角的弧度值等于圓弧的長度除以圓的半徑。因此,當圓弧的長度等于圓的半徑時,這個圓弧的圓心角就稱為1弧度(符號:rad)的角。
360°=2πrad,180°=πrad。
當圓弧的圓心角為θrad時,弧長公式為:l=rθ。
4. 積和差公式與和差積公式
將和與差轉化為乘積的公式:
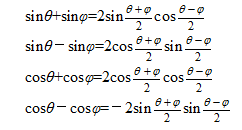
乘積與差值公式:
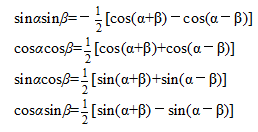
5.利用三角函數尋找極值
若y=2sinθcosθ,則y=sin2θ。可以看出,當θ=45°時,ymax=1。
如果 y = acosθ + bsinθ (a ≠ 0, b ≠ 0),則恒等式變換為:
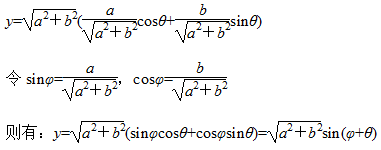
6.常用導數公式
原函數:y=c(c為常數),導數:y'=0;
原函數:y=xn,導數:y'=nx(n-1);

原函數:y=sinx,導數:y'=cosx;
原函數:y=cosx,導數:y'=-sinx;
導數的四種運算:
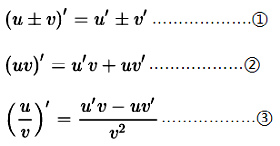
7.常用積分公式
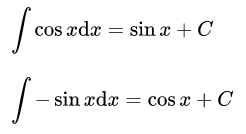
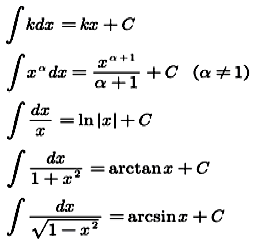
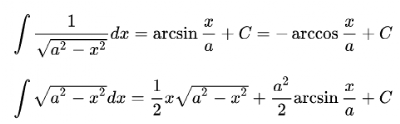
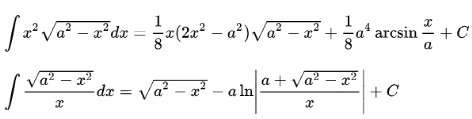
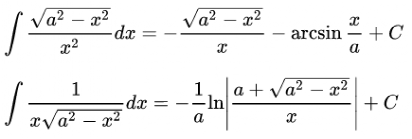
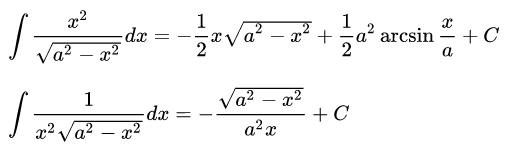
最后需要說明的是,高中物理的學習和解題需要用到大量的數學知識,尤其是初中的數學知識也占了很大的比重,比如關于二次函數、平面幾何、圓與切線、相似三角形、方程與方程組的知識……本文只是列舉了一些同學們最容易陌生但又對物理非常必要的數學知識,大家可以根據自己的實際情況進行補充擴充。
歡迎大家看完點贊、點“正在讀”并轉發分享給更多有需要的朋友,也歡迎大家對作者進行贊賞貝語網校,支持原創。