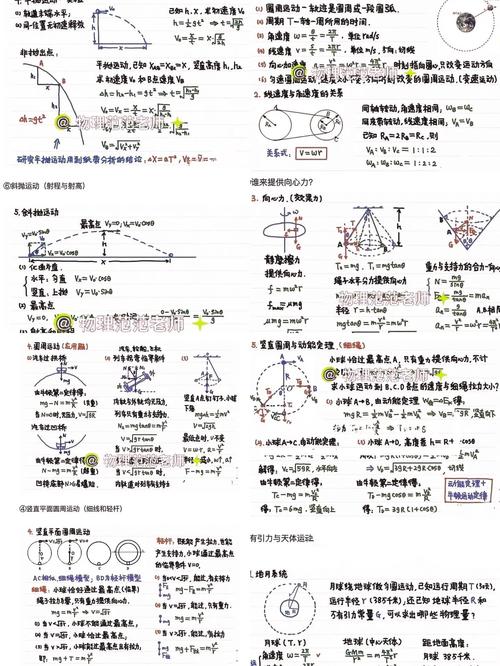
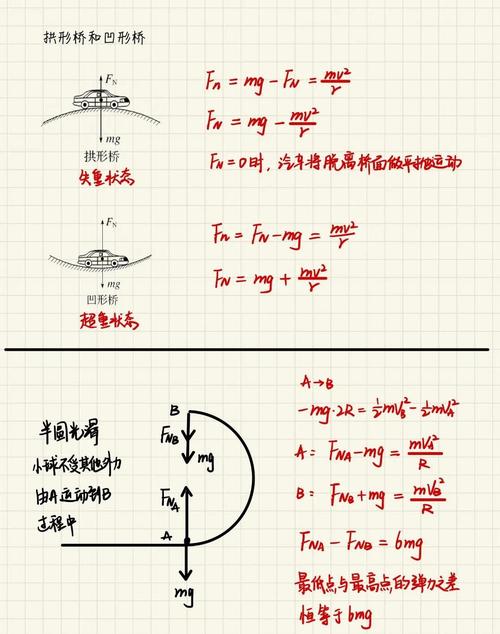
此專題的核心要點是,把重力以及電場力予以合成從而得出“等效重力”留學之路,接著通過類比單一的重力場或者電場當中涉及的運動模型,像是直線運動模型、平拋運動模型以及圓周運動模型來展開分析,其關鍵之處在于要進行受力情況的分析以及運動的分解 。

一、核心受力分析:先判斷“重力是否需要考慮”
這是解題第一步,直接決定后續分析方向:
具備必須考慮重力這一特性的粒子,涵蓋宏觀帶電體,像其中包含的帶電小球啦,還有液滴以及塵埃等,當題目沒有明確表明“忽略重力”這種情況的時候呢,那么意味著重力以及電場力都被認作是受力的范疇 。
能被忽略重力的粒子是微觀帶電粒子高中物理電場問題題目,像電子、質子、α粒子、離子這類,當題目沒有明確表明“考慮重力”的時候,只對電場力進行分析,。
二、三大典型運動模型
1. 直線運動(勻速/勻變速)

2. 類平拋運動

示例:
有一個帶著正電的小球,以水平方向的初始速度 v_0 進入到那種水平方向是向左的勻強電場之中,小球在豎直方向會受到重力的作用,在水平方向會受到電場力的作用,其運動被分解成為水平方向的勻變速運動以及豎直方向的自由落體運動 。
3. 類圓周運動
核心條件:
粒子于“重力加上勻強電場”的環境里,受到細線或者軌道的約束從而做圓周運動,其等效重力呈現恒定狀態,參照重力場之中的圓周運動來剖析“臨界位置”。
關鍵分析點:
重力mg,電場力qE,二者矢量和,是等效重力G',其方向則是“等效重力方向”。
2. 臨界位置(類比“最高點”):

示例:
帶有負電的小球,處于“豎直向上的勻強電場”這個環境里,通過細線進行懸吊從而做圓周運動,其等效重力的方向存在兩種可能情況,當mg大于qE時,等效重力方向是豎直向下,倘若qE大于mg,其所等效重力方向則是豎直向上,要先把等效重力方向給確定下來,之后再去找出臨界位置。
三、解題通用步驟
進行受力分析,要清晰確定重力,還要明確電場力,其大小為F等于qE高中物理電場問題題目,方向是正電荷情況下與電場方向一致,負電荷時則相反,而后計算合外力。
判斷運動的類型,依據“初速度方向”跟“合外力方向”之間的關系,進而確定到底是直線運動,還是類平拋運動,亦或是類圓周運動。
3. 選規律求解:

類平拋,進行正交分解,分別運用“勻速規律”來列方程,再分別運用“勻加速規律”來列方程,之后聯立時間t進行求解。
類似圓周的情況,要先去尋找等效重力以及臨界位置情況喔呢,接著運用“向心力公式”來求取臨界速度呀,之后還得結合動能定理,也就是合外力做功等于動能變化這個原理,去分析其他位置呢。
