靜電場是什么這一概念是,因靜止的電荷而產生的電場,它有著這樣的特點,它起始于正電荷或者無窮遠之處高中物理電場特點,會終止于負電荷或者無窮遠之處。中點電荷的電場具備球對稱性,其表達式是E=kQ/R2,靜電場是滿足疊加原理的。
電場力,是電場針對處于內里的電荷所施加的作用力,其定義式為F=qE,此關系式同時也是電場的定義式,能夠用以計算任意電場對電荷的作用力。特別而言,點電荷的電場針對點電荷的作用力依據庫侖力公式計算,即F=kQq/R2,其方向按照兩電荷的極性予以判斷。電場最為重要的性質是,對處于其中的電荷存在電場力的作用。至于電場力的性質借助電勢加以描述。
電場線,它是為能直觀地去描述靜電場而被人為引入的,它具備這樣一些特點,電場線指示著電勢降低的方向,電場線于某一點處的切線方向是該點電場的方向,電場線不會相交,電場線的疏密程度用來描述電場的大小 。

電勢能,如同物體處于重力場里會具備重力勢能那般,處于電場中的電荷存有電勢能,其定義為:電荷的電勢能等同于將它從該點移至電勢能零點時電場力所做的功。定性而言,我們曉得重力對物體做功時物體的重力勢能會減小,重力做負功時重力勢能會增加貝語網校,而且做功的大小僅與初始位置以及末位置相關,和過程并無關聯,相對應地,電荷q的電勢能E=qUab=q(φ1-φ2),其中φ是電勢,由產生電場的電荷源所決定,恰似g由地球決定一樣。根據電勢能的定義式能夠看出,要是q是正的,那么電荷的電勢能會隨著電勢的升高而變大,假如q是負的,情況恰好相反。
電勢呢,它是由那個產生電場的電荷來決定的,是這樣的情況,就是通常會選取無限遠處的電勢當作零,那么正電荷所具有的電勢是大于零的高中物理電場特點,負電荷所具有的電勢是小于零的。點電荷的電勢表達式是φ=kQ/R ,從電勢的大小通過其表達式能夠看出來,距離電荷源越近的時候它就越大,距離電荷源越遠的時候它就越小 。
提到帶電粒子于電場里的運動,無非是借助電場對電荷的作用使其加速或者偏轉,其具備的特點跟重力對物體做功頗為相似,加速的階段存在Ek=qU,這里的U是兩極板之間的電壓,偏轉階段類似重力場中物體進行的平拋運動,垂直于電場方向呈現勻速直線運動狀態,沿著電場方向是勻加速或者勻減速直線運動狀態。
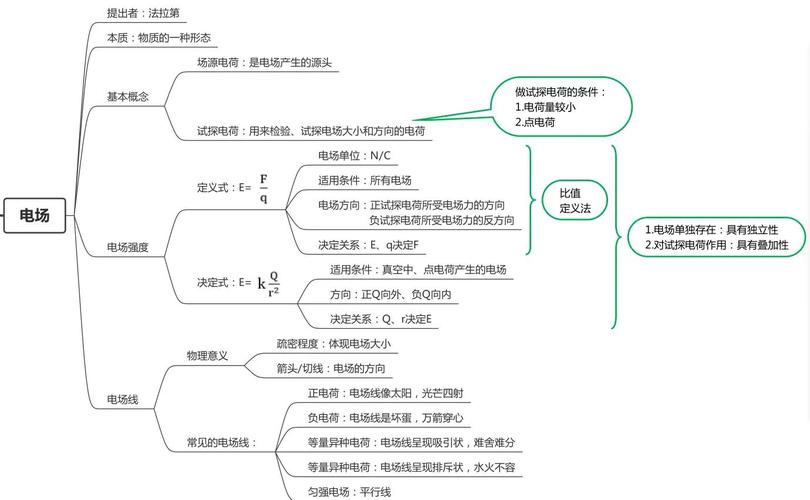
以上是這一章的重點內容吧。
帶電粒子有關電勢的問題拿來借助定義式予以判斷,將其類比成重力勢,這樣做對理解以及運算會有所幫助。電勢高低的判斷辦法是:沿著電場線所指方向電勢會降低,先把電場方向確定好,如此就能明晰電勢方面的方向。帶電粒子的運動狀態依據F=qE來判斷其具體運動情形。
