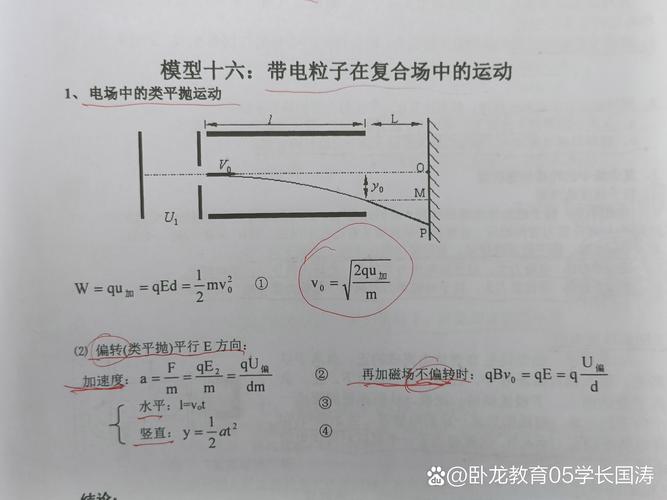
2、偏轉(zhuǎn)運動
處于勻強電場里的帶電質(zhì)點做的偏轉(zhuǎn)運動屬于運動學范疇的問題,其解題所依據(jù)的情況如下:
我們來解析一道題:
題目中提到,示波器能夠被看作是加速電場跟偏轉(zhuǎn)電場的組合,已知其中前者的電壓是U1,后者電壓是U2,接著又說極板長度算L、板間距為d,并且強調(diào)電子加速之前初速能夠忽略不計,那么示波器的靈敏度(也就是偏轉(zhuǎn)電場里每單位偏轉(zhuǎn)電壓所引發(fā)的偏轉(zhuǎn)量h/U2)和加速電場、偏轉(zhuǎn)電場的關(guān)系是正確的是()。
A.L越大,靈敏度越大B. d越大,靈敏度越大
C. U1越大,靈敏度越小 D. 靈敏度與U1無關(guān)
解析:設(shè)電子加速后以速度V0進入偏轉(zhuǎn)電場,則:
對于偏轉(zhuǎn)過程,有:
由此可知AC選項正確。
我們再看一道“正宗”的偏轉(zhuǎn)問題:
如圖甲所示高中物理電池偏轉(zhuǎn)題目留學之路,平行金屬板A與B之間的距離是d,它們的右端放置著垂直于金屬板的靶MN,當下在A、B板上施加乙圖所示的電壓,該電壓的正向值是U0,反向值為U0/2,并且每隔T/2就會換向一次,現(xiàn)有質(zhì)量為m的帶正電且電量為q的連續(xù)粒子束從AB的中點O沿著平行于金屬板的方向OO/射入,設(shè)粒子能夠全部打在靶上而且所有粒子在A、B間的飛行時間均為T,不計重力高中物理電池偏轉(zhuǎn)題目,試問:
(1)在距靶的中心O/點多遠的范圍內(nèi)有粒子擊中?
(2)需讓粒子全部都能打在靶MN之上,那么電壓U0的數(shù)值究竟應(yīng)該符合什么樣的條件呢?(只需寫出U0、m、d、T、q之間的關(guān)系式就行) 。
解析:有粒子,于t=0時刻進入,此粒子打在O/N上,并且其距離是最遠的,還有粒子,在t=T/2時刻進入,該粒子打在O/M上,而且其距離也是最遠的。——物理過程的時間、空間。
(1)有這樣一個情況,在時間等于0的時刻進入的粒子,在從0至T/2這段時間內(nèi)的偏轉(zhuǎn)距離是y1,其加速度為a1 ;該粒子在從T/2至T這段時間偏轉(zhuǎn)的距離是y2,加速度是a2 ;在這種情形下則有:
所以,打在O/N上的最遠距離y下為:
設(shè)定在t等于T除以2這個時刻進入的粒子,于T除以2至T這段時間內(nèi)的偏轉(zhuǎn)距離是y1/ ,其加速度為a1/ ,隨后在T至3T除以2這段時間偏轉(zhuǎn)的距離為y2/ ,加速度為a2/ ,那么:。
所以,打在O/M上的最遠距離y上為:
所以有粒子擊中的范圍內(nèi)為:
由(1)當中的結(jié)果能夠知道,要使得粒子全部都打在靶MN之上,應(yīng)當滿足:
即:
因為上述解析表明,時間以及空間要正確對應(yīng)物理過程,這才是正確解題的前提條件,是這樣的情況 。
我們再來看看一個基本模型:
粒子帶電量為q,其以速度V從兩平行金屬板中心a射入,金屬板長為L、間距為d,粒子沿直線從b穿出,情況如圖甲所示,若把兩金屬板接交流電源,交流電壓隨時問變化規(guī)律如圖乙所示,要使該粒子仍能從b點以入射速度V穿出,那么交流電壓的周期T、板間距d、粒子從a點射入金屬板的時刻應(yīng)滿足啥關(guān)系呢?
解析:要是粒子還能夠從b點以入射時候的速度V穿出去,那么粒子在發(fā)生偏轉(zhuǎn)行進當中必然得歷經(jīng)加速、減速、朝著相反方向加速、朝著相反方向減速到零這四個階段,也就是說粒子進入電場的那個時刻t一定要滿足:
物理過程的時間、空
粒子的軌跡如圖所示:
顯然,有:
在空間關(guān)系這個范疇之中,假定粒子加速的那個階段位移標稱為y1,那么就會出現(xiàn)這樣的情況:d除以2的結(jié)果大于2與y1相乘的積 。
結(jié)合:
可解得:
在擁有了關(guān)于時間以及空間對應(yīng)性的認識之后,于處理設(shè)計型試題之時便能夠做到有的放矢。接下來再去看一道極為經(jīng)典的題目:
設(shè)存在這樣一個例題,呈現(xiàn)出的情況是,在如圖甲所示的狀態(tài)下,處于真空室里的電極K所發(fā)出的電子,其初始速度是不計的,這些電子經(jīng)過電壓U0等于1000V的加速電場隨后之后呢,它會借著小孔S沿著兩水平放置的金屬板A、B間的中心線射進去。其中A、B板的長度L是0.20m,它們之間相距d為0.020m,施加在A、B兩板間的電壓u會隨著時間t產(chǎn)生變化,呈現(xiàn)出的u-t圖線就如同圖乙所示。并且設(shè)定,A、B間的電場能夠被看成是均勻的,而且兩板之外是不存在電場的。電子通過電場區(qū)域的時間極短,在此期間,電場被視作恒定,兩板右側(cè)放置著記錄圓筒,筒的左側(cè)邊緣與極板右端的距離為b,其中b等于0.15m,筒圍繞其豎直軸做勻速轉(zhuǎn)動,其周期T為0.20s,筒的周長s是0.20m,筒能夠接收到通過A、B板的所有電子。

于t等于0時,通過觀察圖乙可知,此時u等于0,將此點(電子打到圓筒記錄紙上的該點)作為xy坐標系的原點,并且選取y軸方向為豎直向上,嘗試計算電子打到記錄紙上的最高點時,其y坐標的值以及x坐標的值,此過程不計重力作用。
(2)在給出的,坐標紙上,也就是圖丙,進行定量地畫,畫出的是電子打到記錄紙上的點,所形成的圖線。
解析:(1)設(shè)電子電量為e,以初速度V0進入偏轉(zhuǎn)電場,則:
把位置定在記錄紙上的最高之處的電子是從板的邊緣上面射出來的,假定電子于電場里運動的時間是t0,存在如此的情況:
由以上各式可解得:
若電子出電場時豎直方向速度為Vy,則有:
設(shè)電子打在最高點的坐標為y,如圖所示,則有:
從u-t圖上可以看出,在Δt的時間內(nèi)有電子射出:
所以,第一個打在最高點的電子的x坐標為:
(2)第二個打在最高點的電子的x坐標為:
第三個打在最高點的電子的x坐標為:
具有20cm周長的圓筒,故而,第三個于最高點被打中的該類電子,同第一個達成了重合。鑒于此圓筒處于勻速轉(zhuǎn)動這樣的狀態(tài),此類電子所留下的痕跡呈現(xiàn)為線性模樣,狀態(tài)如同圖示那般。
當年,本題難得讓一大批考生都被難住了,到了現(xiàn)在進行解析的時候,不難發(fā)覺,不管問題有多么復(fù)雜,其實也都是由一個個簡單問題通過“耦合”這種方式組合而成的 。
祝同學們進步!
