普通高中階段的物理學(xué)科里面的電磁場部分,在這一章節(jié)當(dāng)中講解一道涉及到帶電粒子于電磁場里邊整個(gè)運(yùn)動過程所形成的運(yùn)行軌跡方面的問題 。
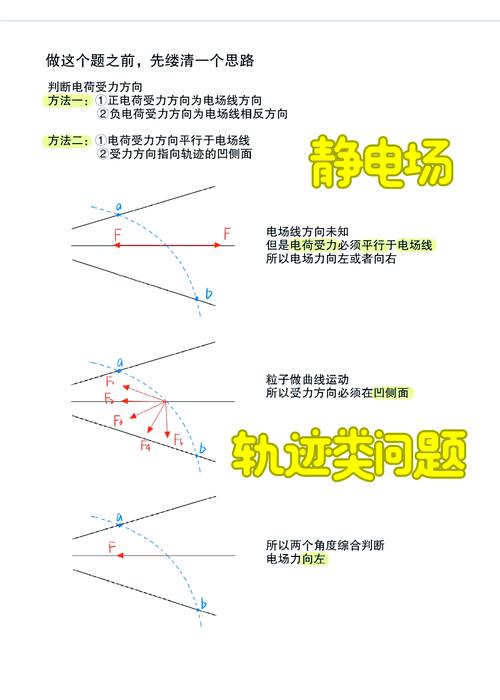
要準(zhǔn)備開講之前,先行去回顧一番,關(guān)于那具有三個(gè)角度的問題。在知悉了解清楚這有著三個(gè)角度的問題之后,如此這般,這道題目便不再是困擾人的問題了。
三個(gè)角度
這三個(gè)角度,其一為弦切角,其一為速度偏轉(zhuǎn)角,其一為圓心角。 要記住高中物理電磁電場公式,圓心角等同于速度偏轉(zhuǎn)角,此二者又均為弦切角的二倍。
直到這層關(guān)系這道題就簡單多了。
下面看題目:
高中物理電磁場
此一過程整體來講是相較簡單的,于電場之中進(jìn)行初速度為零的勻變速式直線運(yùn)動這樣子的情況,能夠運(yùn)用動能定理將此一過程予以表示出來。
關(guān)鍵是在磁場中的圓周運(yùn)動,這個(gè)就需要用到三個(gè)角度的關(guān)系了。

先瞧選項(xiàng)AB部分,有一種粒子呈現(xiàn)垂直于CM而出的情況,此情形實(shí)際上并未運(yùn)用到那三個(gè)角度之間的關(guān)聯(lián)關(guān)系。所依靠的乃是切線所具備的性質(zhì),也就是經(jīng)過切點(diǎn)的半徑會垂直于切線。而這里的切線恰恰契合速度指向的方向由此可知,鑒于在o點(diǎn)處速度是豎直朝著下方的態(tài)勢,能夠推斷出圓心處于x軸之上,再依據(jù)垂直于CM射出此條件,又能夠知曉圓心同樣處于CM之上,進(jìn)而能夠明確圓心就是C點(diǎn),由此便得出半徑為a,借由半徑公式并結(jié)合在電場當(dāng)中呈現(xiàn)的勻變速直線運(yùn)動這種狀況,輕輕松松就能夠把h求解出來了。
關(guān)鍵點(diǎn)在于CD選項(xiàng),它平行于x軸,這就意味著末速度是水平方向的,進(jìn)而速度偏轉(zhuǎn)角為90°,這樣很容易得出弦切角為45°貝語網(wǎng)校,過o點(diǎn)做與速度夾角等于45°的直線就行,呵呵,剛好COM是等腰直角三角形,由此可知粒子從CM中點(diǎn)射出,并且圓心在CO中點(diǎn),從而能夠得到半徑為a/2,之后算法和之前一樣高中物理電磁電場公式,不過也可以不經(jīng)過計(jì)算直接得出結(jié)果 。
詳細(xì)講解請看視頻
高中物理電磁場,利用三個(gè)角度,快速搞定軌跡圓心以及半徑大小
2. (多選),如下這般展現(xiàn),于x軸的上方存在著沿著y軸負(fù)方向的勻強(qiáng)電場,此電場的電場強(qiáng)度為E ,在那x軸下方有著等腰直角三角形CDM區(qū)域所在地方,在此區(qū)域內(nèi)存在著垂直于xOy平面向外的勻強(qiáng)磁場,該磁場的磁感應(yīng)強(qiáng)度為B ,其中C、D處于x軸之上,它們抵達(dá)原點(diǎn)O的距離都為a 。現(xiàn)在將質(zhì)量是m、電荷量為+q的粒子從y軸那里的P點(diǎn)由靜止?fàn)顟B(tài)予以釋放,設(shè)定P點(diǎn)到O點(diǎn)的距離是h ,不考慮重力作用以及空氣阻力所帶來的影響 。如下說法屬于正確范疇之內(nèi)的是,選項(xiàng)為A,其情況是若其中粒子呈現(xiàn)以垂直于CM的狀態(tài)而射出磁場,那么h等于;選項(xiàng)為B,此情形是若粒子以垂直于CM的狀態(tài)射出磁場,那么h等于me;選項(xiàng)為D當(dāng)粒子以平行于x軸的狀態(tài)導(dǎo)出磁場時(shí)那么對應(yīng)的是h42a9的情況;選項(xiàng)為C,在于若粒子以平行于x軸的狀態(tài)射出于磁場時(shí),那么AB方面對應(yīng)的是2a4的情況 。
